Question

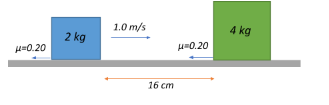
The frictional coefficient between the horizontal surface and each of the blocks shown in the figure is 0.20. The collision between the blocks is perfectly elastic. Find the separation between the two blocks when they come to rest. Take $g = 10ms^{-2}$

Answer 1

First consider only the 2kg block in motion. Using the work energy theorem which suggests that the work done by the frictional force here will be equal to the change in the kinetic energy of the block, find the velocity that the 2kg block gains before colliding with the 4kg block. Given that the elastic collision conserves both momentum and energy of the system, arrive at expressions that can be solved to obtain the velocity of the two blocks upon collision.

Following this, apply the work energy principle now to each of the blocks to obtain the distance they travel before coming to rest. Add up these distances to arrive at the separation between them, which is what we need to this end.

Complete answer:
Frictional force $F_{f} = -\mu mg$
Work-energy theorem: $W_{net} = \Delta KE$
Complete Solution Step-by-Step:
Let the initial velocities of the 2kg and the 4kg blocks before collision be $u_1 =1\;ms^{-1}$ and $u_2=0$ respectively.
The frictional force acting on the 2kg block is given as: $F_{f} = -\mu mg$, where the negative sign indicates that it acts opposite to the motion of the block.
The work done by this frictional force in impeding the motion of the 2kg block as it travels a distance of $s = 16\;cm = 0.16\;m$ is given as:
$W = F_{f}.s = -\mu mg \times s = -0.20 \times 2 \times 10 \times 0.16 = -0.64\;Nm$
The kinetic energy possessed by 2kg block initially is $KE_i = \dfrac{1}{2}mu_1^2 = \dfrac{1}{2}\times 2 \times 1^2 = 1\;J$
If the velocity of the 2kg block after travelling $0.16\;m$ is $v$, then the kinetic energy possessed by the block after it covers a distance of $0.16\;m$ is $KE_f = \dfrac{1}{2}mv^2 = \dfrac{1}{2}\times 2 \times v^2 = v^2\;J$
Now, according to the work energy theorem, the work done by the frictional force is equivalent to the change it imparts to the kinetic energy of the moving 2kg block.
Thus, we have $W = \Delta KE = KE_f – KE_{i}$
$-0.64 = v^2 – 1 \Rightarrow v^2 = 0.36 \Rightarrow v= 0.6\;ms^{-1}$
Now, we are given that the collision between the blocks is elastic. This means that both momentum and kinetic energy are conserved quantities.
Let the velocities of the $m_1=2\;kg$ and $m_2=4\;kg$ blocks after collision be $v_1$ and $v_2$ respectively.
Since the momentum of the system is conserved,
$p_i = p_f$, where $p_i$ and $p_f$ are the total initial and final momenta of the system respectively.
$\Rightarrow m_1v + m_2u_2= m_1v_1 +m_2v_2$
$\Rightarrow (2\times 0.6) +(4 \times 0) = 2v_1 +4v_2 \Rightarrow 2v_1 + 4v_2 =1.2 \Rightarrow v_1 +2v_2 = 0.6 \Rightarrow v_1 = 0.6-2v_2$
Since the kinetic energy of the system is conserved:
$KE_i = KE_f \Rightarrow \dfrac{1}{2}(m_1v^2 +m_2u_2^2) = \dfrac{1}{2}(m_1v_1^2 + m_2v_2^2) \Rightarrow (2\times 0.6^2 + 4 \times 0^2 = 2v_1^2 + 4v_2^2)$
$\Rightarrow 2v_1^2 +4v_2^2 = 0.72 \Rightarrow v_1^2 + 2v_2^2 = 0.36$
Substituting for $v_1 = 0.6-2v_2$ in the above equation, we get:
$(0.6-2v_2)^2 +2v_2^2 = 0.36 \Rightarrow (0.36 + 4v_2^2 – 2.4v_2) + 2v_2^2 = 0.36 \Rightarrow 6v_2^2 = 2.4v_2 \Rightarrow v_2 = \dfrac{2.4}{6} = 0.4\;ms^{-1}$
Since $v_1 = 0.6-2v_2$,
$\Rightarrow v_1 = 0.6 – 2 \times 0.4 = 0.6 – 0.8 = -0.2ms^{-1}$, where the negative sign indicates that the 2kg block retorts back after collision.
We can now apply the work energy theorem to each of the blocks when they come to rest to determine the distance they travel after collision.
For the 2kg block: Assuming it travels a distance $s_1$ after collision, the work done by the frictional force in impeding the motion of the block as it travels through distance $s_1$ will be:
$W = \dfrac{1}{2}m(0)^2 - \dfrac{1}{2}mv_1^2 \Rightarrow F_f \times s_1 = \dfrac{1}{2}.2.(0-0.2^2 ) \Rightarrow (0.2\times 2 \times 10 \times s_1) = 0.04$
$\Rightarrow s_1 = \dfrac{0.04}{4} = 0.01\;m =1\;cm$
For the 4kg block: Assuming it travels a distance $s_2$ after collision, the work done by the frictional force in impeding the motion of the block as it travels through distance $s_2$ will be:
$W = \dfrac{1}{2}m(0)^2 - \dfrac{1}{2}mv_2^2 \Rightarrow F_f \times s_2 = \dfrac{1}{2}.4.(0-0.4^2 ) \Rightarrow (0.2\times 4 \times 10 \times s_2) = 0.32$
$\Rightarrow s_2 = \dfrac{0.32}{8} = 0.04\;m =4\;cm$
Therefore, the separation between the two blocks after collision will be: $s_1+s_2 = 1 +4 =5\;cm$

Note:
Always remember to account for all forces while considering the work done by the forces acting in the system. All forces here, mean those forces that contribute to changing the kinetic energy of the moving body, which is why we considered only the frictional force acting on the blocks in the problem.
Also, do not forget that in:
A. Perfectly elastic collision: momentum and energy are conserved.
B. Inelastic collision: only momentum is conserved.
C. Perfectly inelastic collision: only momentum is conserved but the colliding bodies coalesce together after collision.
But in any type of collision, the total energy of the system is conserved.