Question
Question: The frictional coefficient between the board and the floor shown in the figure is \(\mu\). Find the ...
The frictional coefficient between the board and the floor shown in the figure is μ. Find the maximum force that the man can exert on the rope so that the board does not slip on the floor.
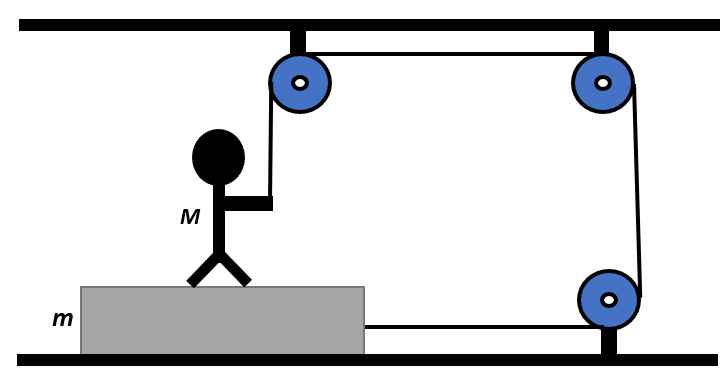
Solution
The board slips when it overcomes the frictional force between it and the floor. In such a case, the maximum force that can be applied by the man in order to just prevent the board from slipping will be equal to the gravitational force. To this end, determine the frictional force acting between the board and the floor to arrive at an expression for the maximum force applied.
Formula used:
Weight W=mg
Frictional force fr=μN
Complete step-by-step answer:
We are given that the coefficient of friction between the board and the floor is μ. The maximum forceF that the man can exert on the rope so that the board does not move or slip along the floor will be equal to the frictional force acting between the board of the floor. This is because the board can slip only when it overcomes the frictional force, so the maximum force that the man can pull the rope with will be the frictional force that he needs to overcome to keep the board on the precipice of slipping.
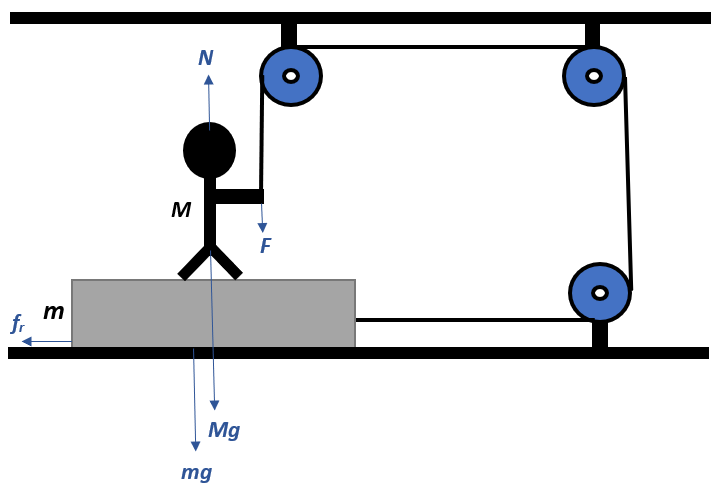
We summarize the influencing forces as shown in the diagram.
Since the man and the board have mass, they will exert a gravitational force by virtue of their weight on the floor.
Now, as the man of massM pulls the rope with a maximum forceF, the force exerted by him on the board will be:
Fm=Mg−F
The force exerted by the board on the floor will be:
Fb=mg
Therefore, the total force exerted on the floor will be:
Ft=Fm+Fb=(Mg−F)+mg
In response to the force Ft, the floor exerts a normal reaction force of equal magnitude but in a direction opposite to Ft, i.e.,
N=Ft=(Mg−F)+mg
So, the frictional force acting between the board and the floor can be given as:
fr=μN=μ((Mg−F)+mg
We have already established that the maximum forceF that the man can exert on the rope so that the board does not slip along the floor will be equal the frictional force acting between the board of the floor, i.e.,
F=μ((Mg−F)+mg
⇒F=μ(Mg−F+mg)=μ((M+m)g−F)=μ(M+m)g−μF
⇒μF+F=μ(M+m)g
⇒F(1+μ)=μ(M+m)g
⇒F=(1+μ)μ(M+m)g
Therefore, the maximum forceF that the man can exert on the rope so that the board does not slip on the floor can be given as:
F=(1+μ)μ(M+m)g
Note: It is always crucial to sketch out all the influencing forces and the direction through which they act upon objects using free body diagrams. This ensures that all forces are accounted for, and helps determine which forces contribute in which direction. Also, do not forget to include the coefficient of friction while calculating the frictional force that is always proportional to the normal reaction force. Thus, obtaining a free body diagram helps us eliminate the non-influencing forces or the forces that may, in fact, cancel each other out, or additively contribute together.
