Question

The frequency of a sonometer wire is f. The frequency becomes $\dfrac{f}{2}$ when the mass producing the tension is completely immersed in water and on immersing the mass in a certain liquid, frequency becomes $\dfrac{f}{3}$. The relative density of the liquid is:
A. 1.32
B. 1.67
C. 1.41
D. 1.18

Answer 1

Using the relation for the fundamental frequency of a sonometer, determine the expression in all three cases, i.e., without immersion, with immersion in water, and with immersion in fluid. Note that in both cases of immersion, the mass is under the influence of an upward buoyant force proportional to the density of the fluid, and this in turn changes the tension in the sonometer wire, which you can visualize using a simple free body diagram.

Use the relations that you obtain in all three cases by rewriting them and substituting values as needed and you will arrive at the density of the liquid. Remember that the density of water is $1\;gcm^{-3}$.

Formula used:
Fundamental frequency of a sonometer $f = \dfrac{1}{2l}\sqrt{\dfrac{T}{\mu}}$.
Buoyant force exerted by a liquid at rest $F_{B} = m_{liquid}g = V\rho_{liquid} g$

Complete answer:
A sonometer is a device that is used for demonstrating the relationship between the frequency of the sound (f) produced by a plucked string, and the length (l) of the string, the tension (T) in the string and the mass per unit length $\mu$ of the string. This relationship is quantified as:
$f = \dfrac{1}{2l}\sqrt{\dfrac{T}{\mu}}$

We have three cases given in the question.

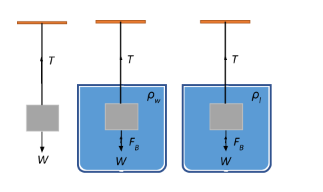
Case 1: When mass producing the tension is subject only to gravity.
In this case, the tension in the string is produced by the gravitational force acting on the mass of the body, which is the weight of the body.
Therefore, the frequency of the sonometer wire is just:
$f = \dfrac{1}{2l}\sqrt{\dfrac{T}{\mu}}$

Case 2: When the mass producing the tension is completely immersed in water.
Let the density of water be $\rho_w$. Let the volume of the mass be $V$. Then, the volume of water displaced by the mass as a consequence of immersing this mass is also $V$.
Therefore, the buoyant force $F_{B}$ exerted by the water on the mass is given as:
$F_{B} = m_{water}g = V\rho_{w} g$, since mass is volume times density.
Therefore, the tension acting in the sonometer wire now becomes:
$T^{\prime} = W -F_B = T – V\rho_w g$
Given that the frequency becomes $\dfrac{f}{2}$:
$\dfrac{f}{2} = \dfrac{1}{2l}\sqrt{\dfrac{T^{\prime}}{\mu}} = \dfrac{1}{2l}\sqrt{\dfrac{T – V\rho_w g}{\mu}}$

Case 3: When the mass producing the tension is completely immersed in another liquid.
Let the density of the liquid be $\rho_l$.
Similar to the previous case, the buoyant force $F_{B}$ exerted by the liquid on the mass is given as:
$F_{B} = m_{liquid}g = V\rho_{l} g$, since mass is volume times density.
Therefore, the tension acting in the sonometer wire now becomes:
$T^{\prime\prime} = W -F_B = T – V\rho_l g$
Given that the frequency becomes $\dfrac{f}{3}$:
$\dfrac{f}{3} = \dfrac{1}{2l}\sqrt{\dfrac{T^{\prime\prime}}{\mu}} = \dfrac{1}{2l}\sqrt{\dfrac{T – V\rho_l g}{\mu}}$
Now, the relative density of the liquid is given as:
$\rho_L = \dfrac{\rho_l}{\rho_w}$
Dividing the two equations of frequency from cases 2 and 3:
$\dfrac{f/2}{f/3} = \dfrac{\left(\dfrac{1}{2l}\sqrt{\dfrac{T – V\rho_w g}{\mu}} \right)}{\left(\dfrac{1}{2l}\sqrt{\dfrac{T – V\rho_l g}{\mu}}\right)}$
$\Rightarrow \dfrac{3}{2} = \sqrt{\dfrac{ T – V\rho_w g }{ T – V\rho_l g }}$
Squaring both sides:
$\Rightarrow \dfrac{9}{4} = \dfrac{ T – V\rho_w g }{ T – V\rho_l g }$

To evaluate further let us find the product Vg in terms of T. For this, divide the frequency equations from cases 2 and 1.
$\Rightarrow \dfrac{f/2}{f} = \dfrac{\left(\dfrac{1}{2l}\sqrt{\dfrac{T – V\rho_w g}{\mu}} \right)}{\left(\dfrac{1}{2l}\sqrt{\dfrac{T}{\mu}}\right)}$
Taking $\rho_w = 1\;gcm^{-3}$ and solving the above equation:
$\dfrac{1}{2} = \sqrt{\dfrac{T-Vg}{T}}$

Squaring on both sides, we get:
$\dfrac{1}{4} = \dfrac{T-Vg}{T} \Rightarrow T = 4T – 4Vg \Rightarrow Vg = \dfrac{3T}{4}$
Substituting this back in our equation, we get:
$\Rightarrow \dfrac{9}{4} = \dfrac{ T – \rho_w \left(\dfrac{3T}{4}\right) }{ T – \rho_l \left(\dfrac{3T}{4}\right) }$
$\Rightarrow \dfrac{9}{4} = \dfrac{4T - \rho_w 3T}{4T-\rho_l 3T}$
$\Rightarrow 9 (4T-\rho_l 3T) = 4 (4T - \rho_w 3T)$
$\Rightarrow 36T – 27\rho_l T = 16T – 12\rho_w T$
$\Rightarrow 36 – 27\rho_l = 16 -12\rho_w$
$\Rightarrow 27\rho_l-12\rho_w = 36-16$
We have $\rho_w = 1\;gcm^{-3}$
$\Rightarrow 27\rho_l = 36-16+12$
$\Rightarrow \rho_l = \dfrac{32}{27} = 1.18\;gcm^{-3}$

So, the correct answer is “Option D”.

Note:
Remember that the magnitude of buoyant force can be derived by calculating the volume of the liquid displaced, though buoyancy is a characteristic of the liquid (and not the immersed body), and is directly proportional to the density of the liquid.
And always use free body diagrams to summarize the list of all influencing forces in a system as this ensures that all forces are accounted for.