Question

The freezing point depression of a 0.10 M solution of formic acid is -0.2046°C. What is the equilibrium constant for the reaction at 298 K?

$HCOO^-(aq) + H_2O(l) \rightleftharpoons HCOOH (aq) + OH^- (aq)$

(Given: $K_f(H_2O) = 1.86K kg mol^{-1}$, Molarity = molality)

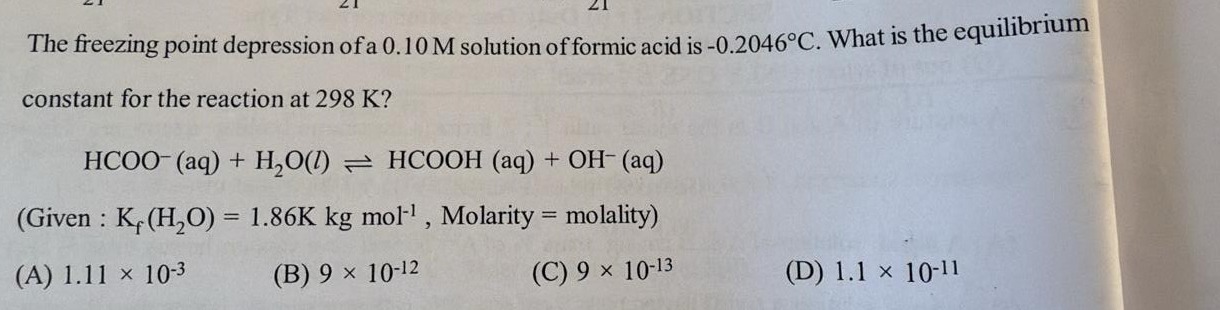
• A. 1.11 × 10-3
• B. 9 × 10-12
• C. 9 × 10-13
• D. 1.1 × 10-11

Answer 1

Answer: (B)

9 × 10-12

Answer 2

Here's how to determine the equilibrium constant for the reaction:

1. Calculate the van't Hoff factor (i):

   • Use the formula: $\Delta T_f = i \cdot K_f \cdot m$
   • Where:
     • $\Delta T_f = 0.2046$ °C (freezing point depression)
     • $K_f = 1.86$ K kg/mol (cryoscopic constant of water)
     • $m = 0.10$ mol/kg (molality of the solution)
   • Solving for $i$: $i = \frac{0.2046}{1.86 \cdot 0.10} = 1.10$

2. Determine the degree of dissociation (α):

   • For a weak acid, $i = 1 + \alpha$
   • Therefore, $\alpha = i - 1 = 1.10 - 1 = 0.10$

3. Calculate the acid dissociation constant ($K_a$) for formic acid:

   • $HCOOH (aq) \rightleftharpoons HCOO^- (aq) + H^+ (aq)$
   • $[HCOOH] = C(1-\alpha) = 0.10(1-0.10) = 0.09$ M
   • $[HCOO^-] = C\alpha = 0.10 \times 0.10 = 0.01$ M
   • $[H^+] = C\alpha = 0.10 \times 0.10 = 0.01$ M
   • $K_a = \frac{[HCOO^-][H^+]}{[HCOOH]} = \frac{(0.01)(0.01)}{0.09} = 1.11 \times 10^{-3}$

4. Calculate the hydrolysis constant ($K_h$):

   • The reaction of interest is: $HCOO^-(aq) + H_2O(l) \rightleftharpoons HCOOH (aq) + OH^- (aq)$
   • $K_h = \frac{K_w}{K_a}$, where $K_w = 1.0 \times 10^{-14}$ (ionic product of water)
   • $K_h = \frac{1.0 \times 10^{-14}}{1.11 \times 10^{-3}} \approx 9 \times 10^{-12}$

Therefore, the equilibrium constant for the reaction is $9 \times 10^{-12}$.