Question

The force $\overrightarrow{F}=\left( {{y}^{2}}-{{x}^{2}}+{{z}^{2}} \right)\widehat{i}+\left( 3xy-5z \right)\widehat{j}+4z\widehat{k}$ is applied on a particle from point $\left( 0,0,0 \right)$ to the point $\left( 2,4,0 \right)$ in the path shown. If ${{W}_{A}},{{W}_{B}},{{W}_{C}}$ are the works done by the force in the paths A, B, C what is the relation between these works done?

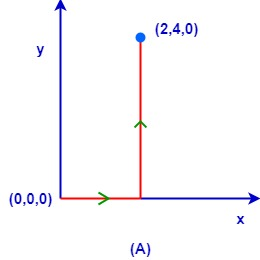
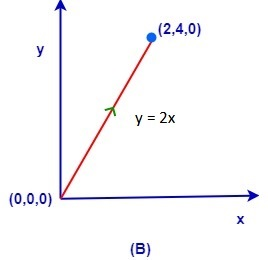
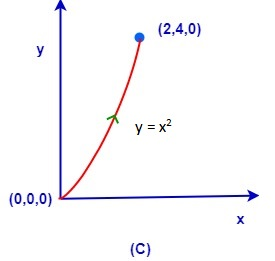
(A) ${{W}_{A}}>{{W}_{C}}>{{W}_{B}}$
(B) ${{W}_{A}}={{W}_{B}}={{W}_{C}}$
(C) ${{W}_{C}}>{{W}_{B}}>{{W}_{A}}$
(D) ${{W}_{B}}>{{W}_{C}}$

Answer 1

Work is done whenever a force moves something over a distance. Work done by a force depends on (1) magnitude of force (2) magnitude of displacement (3) angle between force applied and displacement. Work done by a force to move a particle from one point to the other depends only on the initial and final points and not on the path followed by it.

Complete step by step solution
Work done by force in moving a particle from one point to the other is given by:
$W=F\left( {{r}_{f}}-{{r}_{i}} \right)$
Where ${{r}_{f}}\text{ and }\,{{r}_{i}}$ are the final and initial positions of the particle.
As the Force is the same for all paths.
Also the final and initial points are the same in all the paths.
Therefore, the work done by the force following path A or path B or path C are the same i.e.
${{W}_{A}}={{W}_{B}}={{W}_{C}}$
Hence, option (B) is the correct answer.

Note
We can also verify the above answer by doing actual calculations here but that would just be a mere wastage of time. So it is good to infer that the work done in moving the particle from one point to the other does not depend upon the path followed by it and is the same as far as the initial and final points do not change. You can calculate the energy transferred, or work done, by multiplying the force by the distance moved in the direction of force. This is actual mathematical calculation.