Question
Question: The force on element \( dl \) in the figure at a distance \( l \) from a long wire carrying current ...
The force on element dl in the figure at a distance l from a long wire carrying current I1 is
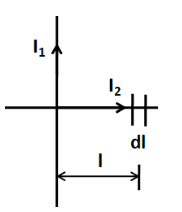
(A) 2πμ0I1I2log(dl)
(B) 2πlμ0I1I2dl
(C) 4πμ0I1I2log(dl)
(D) 4πlμ0I1I2log(dl)
Solution
To solve this question, we need to evaluate the magnetic field at the point where the element is placed. Then, applying the formula of the force on a current carrying conductor, we will get the answer.
Formula used: The formula which is used in solving this question is given by
B=2πrμ0I , here B is the magnetic field produced by a straight current carrying conductor at a perpendicular distance of r from it.
F=I(l×B) , here F is the force acting on a conductor of length l carrying a current I , which is placed in a magnetic field of B .
Complete step by step solution:
We know that the magnetic field due to a straight current carrying wire is given by
B=2πrμ0I (1)
According to the question, we have I=I1 . Also, the element dl is at a distance r=l from the current carrying wire. So putting these in (1) we get
B=2πlμ0I1
From the right hand rule, we get the direction of this magnetic field into the plane of paper.
We know that the force on a current carrying conductor placed in a magnetic field is given by F=I(l×B)
Now, the current in the element is equal to I2 . Also, the length of this element is dl . So the force on this element is
F=I2(dl×B)
As the magnetic field is perpendicular to the current in the element, so we get
F=I2Bdl
From (1)
F=I2(2πlμ0I1)dl
F=2πlμ0I1I2dl
Hence, the correct answer is option B.
Note:
We should not get confused as to why we have taken the magnetic field as uniform for the element dl . As it is of infinitesimally small length, so the variation of the magnetic field over its length is negligible. So, it can be taken as constant.
