Question

The force of gravitation is
(A) Repulsive
(B) Conservative
(C) Electrostatic
(D) Non-conservative

Answer 1

Hint : Observe different properties of gravitational force using the equation of gravitational force. The equation for gravitational force is given by, $F = \dfrac{{GMm}}{{{R^2}}}$ . Where, $m$ and $M$ are the masses of two bodies separated by a distance $R$

Complete Step By Step Answer:
We know that, the gravitational force acting on a body of mass $M$ by a mass $m$ or vice versa separated by a distance $R$ is given by, $\vec F = \dfrac{{GMm}}{{{R^2}}}\hat R$ . Where, $G$ is the gravitational constant.
So, we can see that, $F\alpha \dfrac{1}{{{R^2}}}$ If both the masses are constant. So, the direction of force is the direction of the relative position vector $\vec R$ . So, the Force is a repulsive one.
Hence, option ( A) is correct.

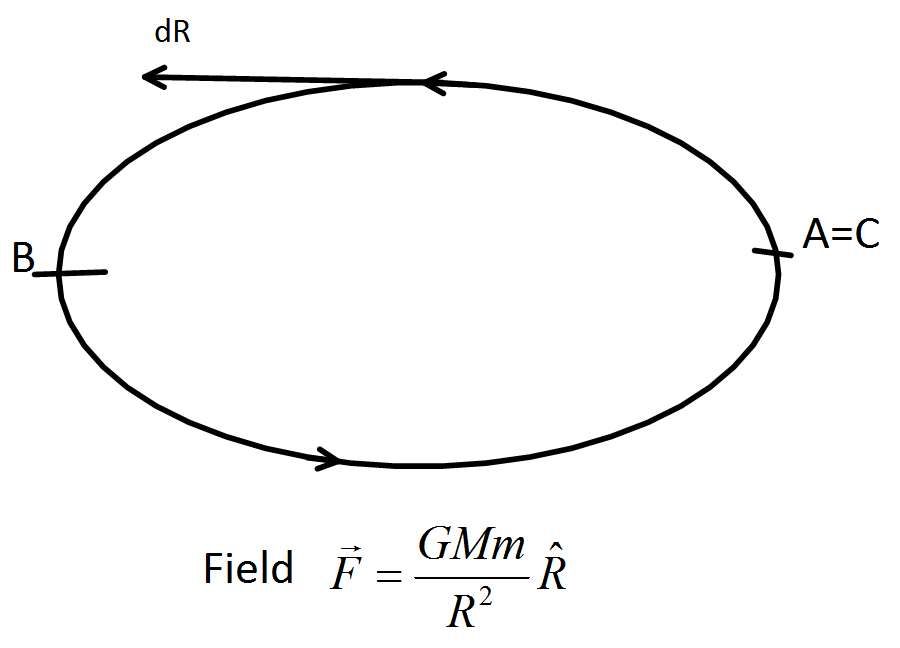
Now, we know, a force field is said to be conserved if the work done over a closed path is zero.
So, let a ABC is a closed path then, work done to take the mass $M$ in a Gravitational force field $\vec F = \dfrac{{GMm}}{{{R^2}}}\hat R$ from A to B is, $W = \int\limits_A^B {F.dR}$
Putting the value of $F$ we get,
${W_1} = \int\limits_A^B {\dfrac{{GMm}}{{{R^2}}}dR}$
$GMm\left[ { - \dfrac{1}{R}} \right]_A^B$
$= GMm\left[ {\dfrac{1}{{{R_A}}} - \dfrac{1}{{{R_B}}}} \right]$
Now work done to take the mass $M$ in a Gravitational force field $\vec F = \dfrac{{GMm}}{{{R^2}}}\hat R$ from A to B is, $W = \int\limits_B^{C = A} {F.dR}$
${W_2} = \int\limits_B^A {\dfrac{{GMm}}{{{R^2}}}dR}$
$= GMm\left[ { - \dfrac{1}{R}} \right]_B^A$
$= GMm\left[ {\dfrac{1}{{{R_B}}} - \dfrac{1}{{{R_A}}}} \right]$
Net work done is ,
${W_1} + {W_2} = GMm\left[ {\dfrac{1}{{{R_A}}} - \dfrac{1}{{{R_B}}}} \right] + GMm\left[ {\dfrac{1}{{{R_B}}} - \dfrac{1}{{{R_A}}}} \right]$
That becomes,
$= GMm\left[ {\dfrac{1}{{{R_A}}} - \dfrac{1}{{{R_B}}} + \dfrac{1}{{{R_B}}} - \dfrac{1}{{{R_A}}}} \right]$
$= 0$
Hence, the gravitational force field is a conservative force field.
Hence, option ( B) is correct and option ( D) is incorrect.
We can see in gravitational force, there is no term for charges hence it cannot be an electrostatic force.
Hence, option ( C) is incorrect.
Hence, option (A) and (B) are correct choices.

Note :
Gravitational force can only be realizable only if one or both of the mass is very large or power of the term $\dfrac{{Mm}}{{{R^2}}}$ is ${10^{11}}$ since, $G = 6.67 \times {10^{ - 11}}N{m^2}k{g^{ - 2}}$ . When the distance is very small (atomic level) gravitational force vanishes, then there are only atomic or nuclear forces.