Question
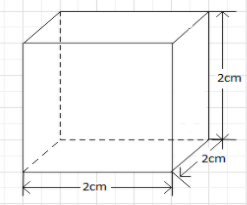
Question: The force needed to punch a hole in a shape of square of edge length 2cm in a steel sheet 2mm thick ...
The force needed to punch a hole in a shape of square of edge length 2cm in a steel sheet 2mm thick is , ( Given: Shearing stress=3.5×108N/m2)
Solution
We have given the shearing stress and asked the force needed to punch a hole, the shearing stress is given as the ratio of force and the cross sectional area. With the help of shearing stress formulas we can find the force required. Before substituting the values the quantity should be changed in metre as the length is in cm and sheet thickness is in mm.
Formula used:
τ=AF
Complete answer:
Shear stress is the force applied along the plane or parallel to the plane such that it deforms the shape of the object. The shearing stress is given as
τ=AF
Where F is force and A is the cross sectional area on which force is applied.
Cross-sectional area is the 2-D area we get after slicing or cutting a 3-D object, it can be sliced in any way either perpendicular to its axis or parallel. Here cross sectional area can be given as
A=4l×t
4l is the perimeter of the cube, l is the edge length and t is the thickness of the steel sheet.
Now the force required here is given as
