Question
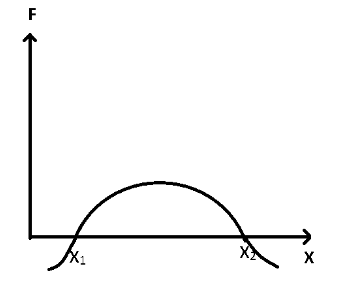
Question: The force acting on a body moving along x-axis varies with the position of the particle as shown in ...
The force acting on a body moving along x-axis varies with the position of the particle as shown in figure. The body is in stable equilibrium at
A. x=x1
B. x=x2
C. both x1and x2
D. neither x1nor x2
Solution
For solving this problem, first we need to know the difference between equilibrium and stable equilibrium. When both, the internal energy and motion of the body does not change with time, the body is called to be in an equilibrium state. However, when the body is displaced from its equilibrium state and still if it tends to move towards the specific equilibrium point, then it is called the stable equilibrium state. Here, we need to find the point where the body tends to return to its original equilibrium point. Therefore, first we will find the equilibrium point and then the stable equilibrium point.
Formula used:
F=−dxdU,
where, F is the force, dU is the change in internal energy and dx is displacement.
Complete step by step answer:
The first step we will do here is to find the equilibrium points.
We know that F=−dxdU
From the given figure, it is clear that the force is zero at both points x1 and x2.
Therefore. at x=x1 and x=x2, F=−dxdU=0
So, we can say that the body is in the equilibrium state at both the points x1 and x2. Now, we need to find at which of these points the body is in stable equilibrium.The condition for the equilibrium to be stable is dxdF<0 which means that the force should be applied in the negative direction to bring the body back to its original equilibrium state.
At x=x1, dxdF>0 which means that force will be in the forward direction and body will not come to its equilibrium state once it is displaced. Thus, at this point the body is not in the stable equilibrium.
Now at x=x2, dxdF<0 which means that force will be in the backward direction and body will come to its equilibrium state once it is displaced. Thus, at this point the body is in the stable equilibrium.
Hence, option B is the right answer.
Note: Here, we have used the concept of stable equilibrium where a body tends to return back to its equilibrium state when displacement occurs. There are three types of equilibrium: stable, unstable and neutral. In unstable equilibrium, the body tends to move away from the equilibrium point when displaced. In neutral equilibrium a body does not move away or towards the equilibrium point and remains still at the equilibrium point.
