Question

The following table shows a record from a hospital of 84 numbers of casualties due to accidents of different age groups.

Age (in years)	5-15	15-25	25-35	35-45	45-55	55-65	65-75
No. of casualties	6	10	15	13	25	8	7

Taking a scale of 2cm = 10 years on one axis and 2 cm = 10 casualties on the other. Draw an ogive and estimate:
(i)The median.
(ii)The upper quartile.
(iii)The number of casualties above 57 years.

Answer 1

To find the median and upper quartile of a given data firstly we have to draw less than type of given data and then we calculate median and upper quartile from the graph.

Complete step-by-step answer:
The given data is continuous and total frequency = 84. The less than type cumulative frequency is given as:

Age ( in years)	Cumulative frequency
Less than 15	6
Less than 25	6 + 10 = 16
Less than 35	16 + 15 = 31
Less than 45	31 + 13 = 44
Less than 55	44 + 25 = 69
Less than 65	69 + 8 = 77
Less than 75	77 + 7 = 84

We draw less than type ogive on graph

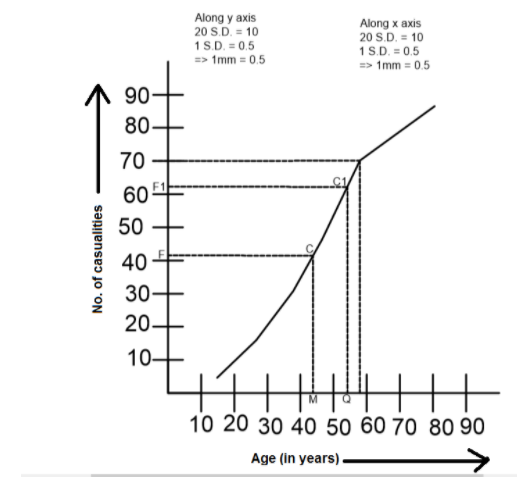
To find Median:
Total frequency = 84 (even)
So the mean of$\;\;\dfrac{N}{2}$ and $\;\;\dfrac{N}{2} + 1$ i.e. the mean of 42 and 43 is 42.5. The point F on Y-axis represents the cumulative frequency of 42.5. Draw Fc II X-axis, which cut the ogive at C. Draw CM Xaxis. The point M represents the median.
So Median = 44
To find Upper quartile $\dfrac{{3N}}{4} = 3 \times \dfrac{{84}}{4} = 63$
The point F2 on the Y axis represents cumulative frequency 63. Drawf1C1 X axis. Which cut the ogive at C1. DrawC1Q ⊥Xaxis. The Point Q represents the upper quartile.
∴ Upper quartile = 53
To find the number of casualties above 57.
Draw line ∥Y axis from (57) which meet at C2. Draw C2F2∥Xaxis . The F2is at 70.5
So, the number of casualties above 57 is 7.

Note: Median is the middle number in a sorted list of numbers and can be more descriptive of that data set than the average.
A quartile is a statistical term that describes a division of observations into four defined intervals based on the values of the data and how they compose to the entire set of observations.