Question

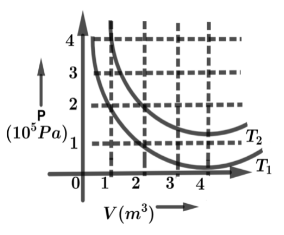
The following graph shows two isotherms for a fixed mass of an ideal gas. The ratio of r.m.s speed of the molecules at temperature ${T_1}$ and ${T_2}$ is:

Answer 1

In the question there given a graph showing the two isotherms for fixed ideal gas, from the given graph we have to find the root mean square of the ratio of ${T_1}$ and ${T_2}$. For this we are using the rms formula for calculating the ratio of speed of molecules.

Complete step by step answer:
Given temperature ${T_1}$ we are calculating the rms value,
Then ${V_1} = \sqrt {\dfrac{{3R{T_1}}}{M}} \to \left( 1 \right)$
For temperature ${T_2}$ the rms value is,
${V_2} = \sqrt {\dfrac{{3R{T_2}}}{M}} \to \left( 2 \right)$
By diving the rms value equation (1) divides (2),
$\dfrac{{{V_1}}}{{{V_2}}} = \sqrt {\dfrac{{{T_1}}}{{{T_2}}}} \to \left( A \right)$
We Have find the rms value for two temperatures,

Now from the graph, the PV are constant in both the temperature curves in graph
So from graph $PV = C$ constant in two temperatures
From graph the temperature ${T_1}$ written as, $2 \times 1 = nR{T_1}$
From graph in temperature ${T_1}$ the curve meets the points $\left( {2,1} \right)$ so that we have written as,
$2 \times 1 = nR{T_1} \to \left( 3 \right)$
Same as for temperature ${T_2}$ curve, where it meets the points in $\left( {2,2} \right)$, so we have written for second temperature ${T_2}$ is
$2 \times 2 = nR{T_2} \to \left( 4 \right)$

Now we are going to divide the equations (3) and (4),
Therefore,
$\dfrac{2}{4} = \dfrac{{nR{T_1}}}{{nR{T_2}}} \\\ \Rightarrow \dfrac{{{T_1}}}{{{T_2}}} = \dfrac{1}{2} \\\$
Now we are substituting the values of ratio of two temperatures in the rms ratio, then we get
$\dfrac{{{V_1}}}{{{V_2}}} = \sqrt {\dfrac{1}{2}}$
We can also write the above equation in,
$\therefore \dfrac{{{V_1}}}{{{V_2}}} = \dfrac{1}{{\sqrt 2 }}$
Thus we have proved the ratio of rms speed of the molecules for two temperatures.

Note: From the given graph only we are proved the ratio of rms speed of the molecules of the temperatures ${T_1}$ and ${T_2}$. To find this ratio first of all we have proven the rms of temperature and then we find the temperature from points taken from X-axis and Y-axis for two temperatures. Then we find the ratio of rms speed of the molecules.