Question
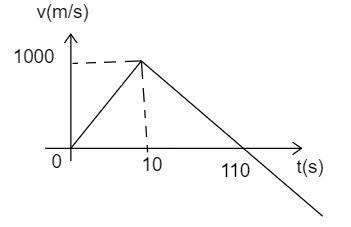
Question: The following graph shows the variation of velocity of a rocket with time. Then the maximum height a...
The following graph shows the variation of velocity of a rocket with time. Then the maximum height attained by the rocket is-
(A) 1.1Km
(B) 5Km
(C) 55Km
(D) None of these
Solution
Analyze the given graph of the velocity versus time. The area covered by the velocity-time graph provides the answer for the maximum height traveled. Use the formula of the area of the triangle given below, apply it to the given graph to find the area covered by the graph.
Formula used:
The area of the triangle is given by
A=21bh
Where A is the area of the triangle, b is the base and h is the height of the triangle.
Complete step-by-step solution:
The given graph in the question represents the velocity of the rocket with respect to time. In order to find the maximum height at which the rocket travels, the integral part of the velocity with respect to time is taken.
hmax=∫vdt
The maximum height is calculated by the area covered under the line vt.
hmax=A
Substituting the area of the triangle in the above step, we get
hmax=21bh
Substitute the value of the base of the triangle and the height of the triangle from the graph of the velocity versus time given.
hmax=21×110×1000
By performing a various arithmetic operation in the above step, we get
hmax=55Km
Hence the maximum height at which the rocket moves is obtained as 55Km.
Thus the option (C) is correct.
Note: Don’t be confused that the maximum height of the rocket is 1000 . This is wrong, it is only applicable when the graph is displacement versus time. Since it is velocity versus time, the highest value 1000 is the maximum velocity value, so it cannot be taken as the maximum height. It is obtained by taking the area covered by the graph.
