Question

The following circuit represents.

$A.$ OR gate
$B.$ XOR gate
$C.$ AND gate

Answer 1

Hint : In order to solve the given question we will see which basic logic gates are present. We need to know that AND gate multiplies the inputs and OR gate adds the inputs.

Complete Step By Step Answer:
Here we have two NOT gates, two AND gates and one OR gate in the given circuit. For simplicity, let’s number the gates $1,2,3,4$ and $5$ . The upper and lower NOT gates are numbered $1$ and $2$ , the upper and lower AND gates are numbered $3$ and $4$ and OR gate is numbered $5$ .

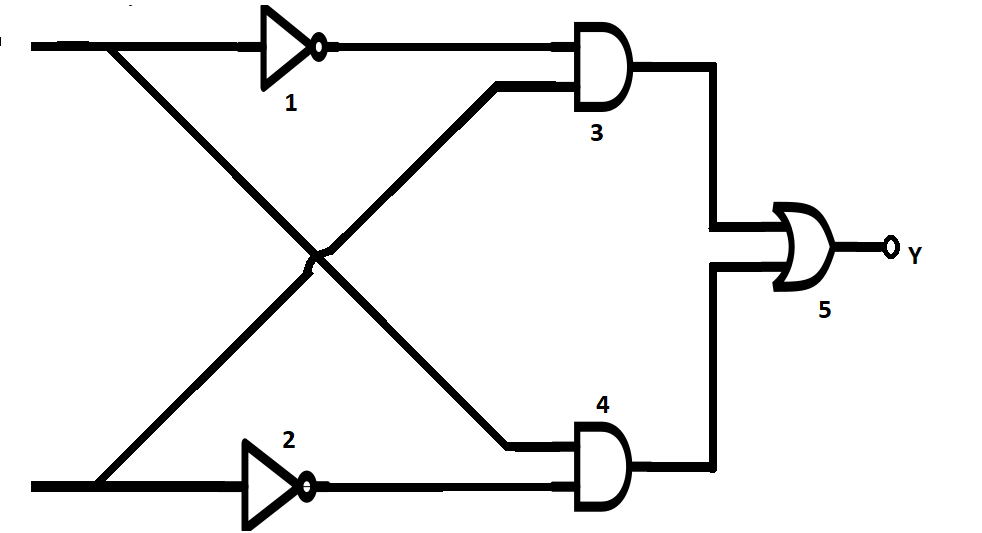
Now let’s look upon the Boolean expressions of the gates. The Boolean expression of the NOT gate is $Y=\bar{A}$ , AND gate is $Y=A\cdot B$ and OR gate is $Y=A+B$ .
Now the output of first NOT gate is ${{Y}_{1}}=\bar{A}$ , output of second NOT gate is ${{Y}_{2}}=\bar{B}$ .
Now for the third AND gate the inputs will be ${{Y}_{1}}$ and $B$ . Similarly, for the fourth AND gate the inputs will be ${{Y}_{2}}$ and $A$ .
Now as we know that AND gate multiplies the inputs, we have output of third AND gate as ${{Y}_{3}}={{Y}_{1}}\cdot B$ and fourth AND gate as ${{Y}_{4}}={{Y}_{2}}\cdot A$ .
Now we also know that OR gate adds the inputs, so we have output of fifth OR gate as $\begin{aligned} & {{Y}_{5}}={{Y}_{3}}+{{Y}_{4}} \\\ & {{Y}_{5}}={{Y}_{1}}\cdot B+{{Y}_{2}}\cdot A \\\ & {{Y}_{5}}=\bar{A}\cdot B+\bar{B}\cdot A \\\ \end{aligned}$
We know that this is the Boolean expression of XOR gate. Therefore, the above circuit represents XOR gate.
Hence, option $(B)$ is the correct answer.

Note :
Logic gates are used to carry out logical operations on single or multiple binary inputs and result in one binary output. Other name for output $1$ is high output and $0$ is low output. One must remember Boolean expressions of respective basic gates while solving logic gates related questions.