Question

The focus and directrix of a parabola are $\left( 0,0 \right)$ and $y=2x+1$. The equation of the axis is:
(a) $2x+y=0$
(b) $x+2y=0$
(c) $x+2y=5$
(d) $x+2y-7=0$

Answer 1

We start solving the problem by finding the slope of the directrix of the parabola by comparing its equation with the standard equation of line. We then use the fact that the axis is perpendicular to the directrix of the parabola and the product of slopes of perpendicular lines is ‘–1’ to find the slope of the axis of parabola. We then recall the property that the vertex and focus of parabola lies on the axis of parabola. We then find the equation of the axis using the fact that the equation of the line passing through the point $\left( a,b \right)$ and having slope ‘m’ is $\left( y-a \right)=m\left( x-b \right)$.

Complete step-by-step answer:
According to the problem, we are given that the focus and directrix of a parabola are $\left( 0,0 \right)$ and $y=2x+1$. We need to find the equation of the axis.

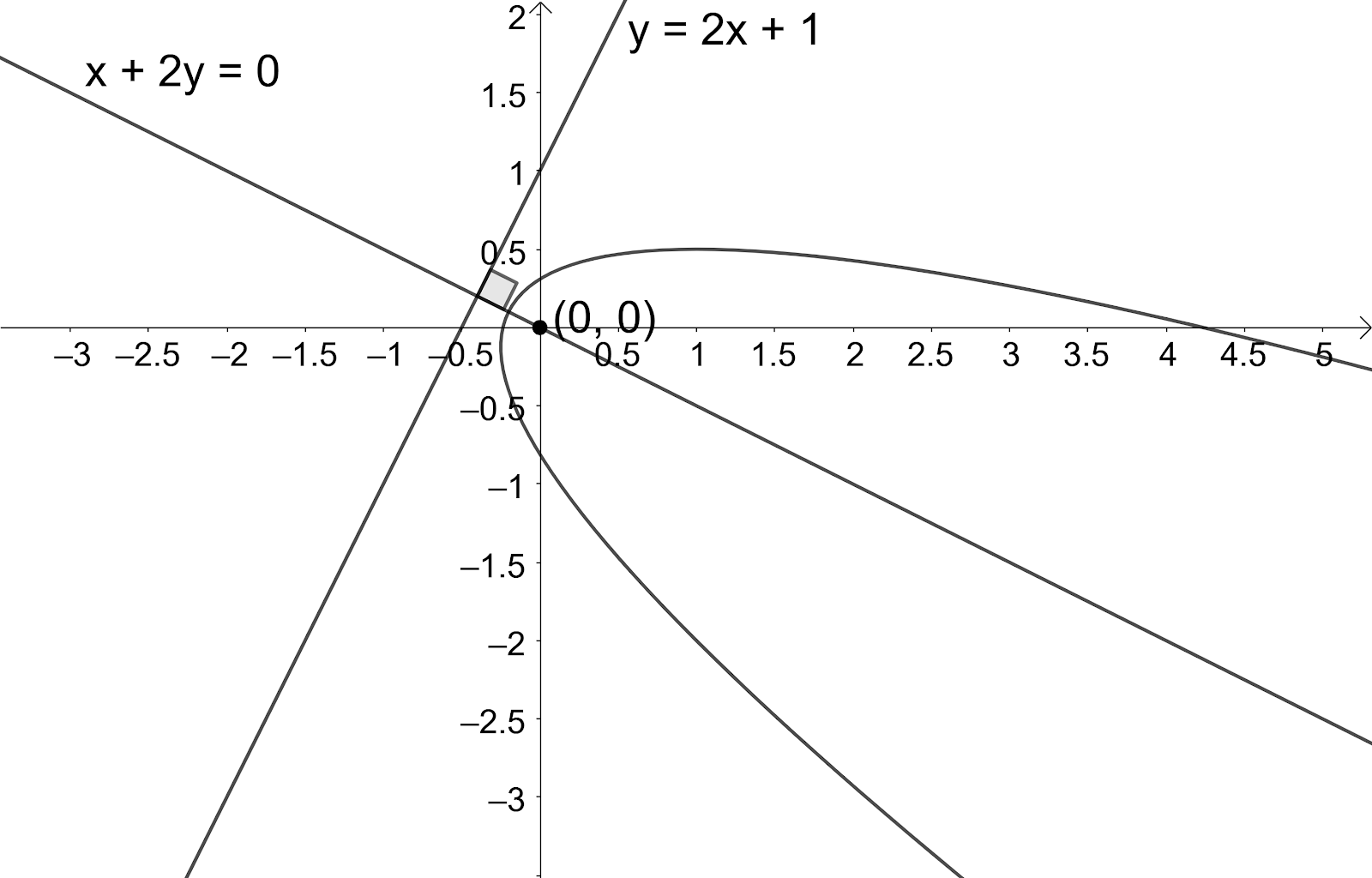
Let us compare the equation of the directrix $y=2x+1$ with the standard equation of line $y=mx+c$. So, the slope of the directrix is $2.$
We know that the axis of the parabola is perpendicular to the directrix of parabola. We also know that the product of slopes of the two perpendicular lines is ‘–1’.
Let us assume the slope of the axis is ‘m’.
So, we have $m\times 2=-1$.
$\Rightarrow m=\dfrac{-1}{2}$ ---(1).
We know that the axis of the parabola passes through the vertex and focus of the parabola.
So, the axis of the parabola passes through $\left( 0,0 \right)$.
We know that the equation of the line passing through the point $\left( a,b \right)$ and having slope ‘m’ is $\left( y-a \right)=m\left( x-b \right)$.
So, the equation of the axis is $\left( y-0 \right)=\dfrac{-1}{2}\left( x-0 \right)$.
$\Rightarrow y=\dfrac{-1}{2}x$.
$\Rightarrow 2y=-x$.
$\Rightarrow x+2y=0$.
So, we have found the equation of the axis of parabola as $x+2y=0$.
The correct option for the given problem is (b).

So, the correct answer is “Option (b)”.

Note: We should not confuse or make calculation mistakes while solving this problem. We should be thorough with the concepts of directrix, focus and vertex of the parabola before solving this problem. We should know that the product of slopes of perpendicular lines (‘–1’) is valid only for non-vertical lines that means if the directrix is parallel to either of the axes we should not use this formula. We can also find the equation of the parabola using the focus and directrix of the parabola. Similarly, we can expect the problem to find the vertex and equation of the tangent at the vertex of the parabola.