Solveeit Logo
Login

Question

Question: The foci of hyperbola \[9{{x}^{2}}-16{{y}^{2}}+18x+32y-151=0\] are (a) (2, 3), (5, 7) (b) (4, 1...

The foci of hyperbola 9x2−16y2+18x+32y−151=09{{x}^{2}}-16{{y}^{2}}+18x+32y-151=0 are
(a) (2, 3), (5, 7)
(b) (4, 1), (– 6, 1)
(c) (0, 0), (5, 2)
(d) None of these

Explanation

Solution

Hint:First of all, convert the given equation into the standard hyperbolic equation of the form (x−h)2a2−(y−k)2b2=1\dfrac{{{\left( x-h \right)}^{2}}}{{{a}^{2}}}-\dfrac{{{\left( y-k \right)}^{2}}}{{{b}^{2}}}=1 and then write the focus of the hyperbola as (h±ae,k)\left( h\pm ae,k \right) where e=1+b2a2e=\sqrt{1+\dfrac{{{b}^{2}}}{{{a}^{2}}}}. Take care while converting the given equation into standard form.

Complete step-by-step answer:
In this question, we have to find the foci of the hyperbola 9x2−16y2+18x+32y−151=09{{x}^{2}}-16{{y}^{2}}+18x+32y-151=0. First of all, let us convert the given equation into the standard hyperbolic equation. We know that the standard hyperbola is of the form (x−h)2a2−(y−k)2b2=1\dfrac{{{\left( x-h \right)}^{2}}}{{{a}^{2}}}-\dfrac{{{\left( y-k \right)}^{2}}}{{{b}^{2}}}=1 where h and k can be any constants. Let us now consider our equation.
9x2−16y2+18x+32y−151=09{{x}^{2}}-16{{y}^{2}}+18x+32y-151=0
By rearranging the terms of the above equation, we get,
(9x2+18x)−(16y2−32y)−151=0\left( 9{{x}^{2}}+18x \right)-\left( 16{{y}^{2}}-32y \right)-151=0
We can also write this above equation as,
[(3x)2+2(3x)(3)]−[(4y)2−2(4y)(4)]−151=0\left[ {{\left( 3x \right)}^{2}}+2\left( 3x \right)\left( 3 \right) \right]-\left[ {{\left( 4y \right)}^{2}}-2\left( 4y \right)\left( 4 \right) \right]-151=0
We know that by adding and subtracting the same constant equation remains the same. So, we get,
[(3x)2+2(3x)(3)+(3)2−(3)2]−[(4y)2−2(4y)(4)+(4)2−(4)2]−151=0\left[ {{\left( 3x \right)}^{2}}+2\left( 3x \right)\left( 3 \right)+{{\left( 3 \right)}^{2}}-{{\left( 3 \right)}^{2}} \right]-\left[ {{\left( 4y \right)}^{2}}-2\left( 4y \right)\left( 4 \right)+{{\left( 4 \right)}^{2}}-{{\left( 4 \right)}^{2}} \right]-151=0
[(3x)2+2(3x)(3)+(3)2]−(3)2−[(4y)2−2(4y)(4)+(4)2]+(4)2−151=0\left[ {{\left( 3x \right)}^{2}}+2\left( 3x \right)\left( 3 \right)+{{\left( 3 \right)}^{2}} \right]-{{\left( 3 \right)}^{2}}-\left[ {{\left( 4y \right)}^{2}}-2\left( 4y \right)\left( 4 \right)+{{\left( 4 \right)}^{2}} \right]+{{\left( 4 \right)}^{2}}-151=0
We know that a2+b2+2ab=(a+b)2{{a}^{2}}+{{b}^{2}}+2ab={{\left( a+b \right)}^{2}} and a2+b2−2ab=(a−b)2{{a}^{2}}+{{b}^{2}}-2ab={{\left( a-b \right)}^{2}}. By using these in the above equation, we get,
(3x+3)2−9−(4y−4)2+16−151=0{{\left( 3x+3 \right)}^{2}}-9-{{\left( 4y-4 \right)}^{2}}+16-151=0
(3x+3)2−(4y−4)2−9+16−151=0{{\left( 3x+3 \right)}^{2}}-{{\left( 4y-4 \right)}^{2}}-9+16-151=0
(3x+3)2−(4y−4)2−144=0{{\left( 3x+3 \right)}^{2}}-{{\left( 4y-4 \right)}^{2}}-144=0
By taking out the common value from the above equation, we get,
9(x+1)2−16(y−1)2−144=09{{\left( x+1 \right)}^{2}}-16{{\left( y-1 \right)}^{2}}-144=0
By dividing 144 in the above equation, we get,
9(x+1)2144−16(y−1)2144=1\dfrac{9{{\left( x+1 \right)}^{2}}}{144}-\dfrac{16{{\left( y-1 \right)}^{2}}}{144}=1
(x+1)216−(y−1)29=1\dfrac{{{\left( x+1 \right)}^{2}}}{16}-\dfrac{{{\left( y-1 \right)}^{2}}}{9}=1
(x−(−1))2(4)2−(y−1)2(3)2=1\dfrac{{{\left( x-\left( -1 \right) \right)}^{2}}}{{{\left( 4 \right)}^{2}}}-\dfrac{{{\left( y-1 \right)}^{2}}}{{{\left( 3 \right)}^{2}}}=1
By comparing the above equation by standard equation,
(x−h)2a2−(y−k)2b2=1\dfrac{{{\left( x-h \right)}^{2}}}{{{a}^{2}}}-\dfrac{{{\left( y-k \right)}^{2}}}{{{b}^{2}}}=1
We get, h = – 1, k = 1, a = 4 and b= 3.
Let us first find the eccentricity (e) of this hyperbola, we know that
e2=1+b2a2{{e}^{2}}=1+\dfrac{{{b}^{2}}}{{{a}^{2}}}
By substituting the value of a and b, we get,
e2=1+3242{{e}^{2}}=1+\dfrac{{{3}^{2}}}{{{4}^{2}}}
e2=42+3242=16+916{{e}^{2}}=\dfrac{{{4}^{2}}+{{3}^{2}}}{{{4}^{2}}}=\dfrac{16+9}{16}
e2=2516{{e}^{2}}=\dfrac{25}{16}
Therefore, e=2516=54e=\sqrt{\dfrac{25}{16}}=\dfrac{5}{4}
Now, we know that the focus of the given hyperbola lies at (x,y)=(h±ae,k)\left( x,y \right)=\left( h\pm ae,k \right)
So, we get the first focus as
x=h+aex=h+ae
x=−1+4(54)x=-1+4\left( \dfrac{5}{4} \right)
x=4x=4
y=k=1y=k=1
So, (x, y) = (4, 1)
We get the second focus as,
x=h−aex=h-ae
x=−1−4(54)x=-1-4\left( \dfrac{5}{4} \right)
x=−6x=-6
y=k=1y=k=1
So, (x, y) = (– 6, 1)
We can also draw the given hyperbola as

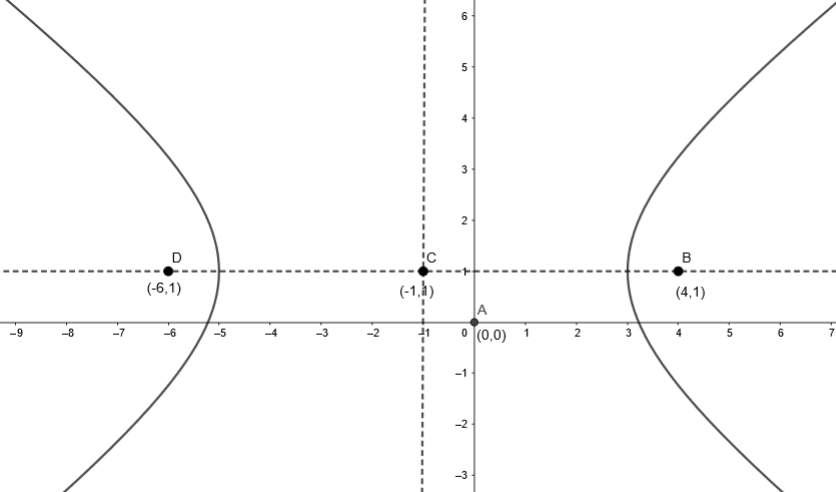
So, option (b) is the right answer.

Note: In this question, some students write the focus as (±ae,0)\left( \pm ae,0 \right) which is wrong as that is true only for h = k = 0. But here, we can see that the vertex of the hyperbola is shifted. So, the focus would also shift accordingly. Also, students must take care that b is the conjugate axis while a is the transverse axis while finding the eccentricity. Also, for hyperbola, e is always greater than 1.