Question

The focal length of an equiconvex lens is equal to the radius of curvature of either face. What is the refractive index of the material of the lens?

Answer 1

In order to find the refractive index, we will use the lens makers formula; in this formula we will put some values according to the given statement which will help us to find the answer. We will put the same value for focal length and radius of curvature to find the refractive index.

Formula Used:
$\dfrac{1}{f} = (\mu - 1)\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)$

Complete step-by-step answer :
Firstly , Let us try to understand what do we exactly mean by an equiconvex lens.
Equiconvex lenses are those whose both the refracting surfaces have the same or equal radius of curvature. We can also see both the sides are convex as shown in the figure.

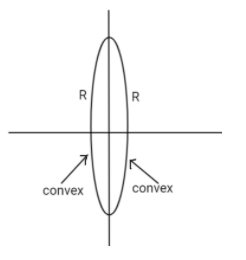
As we know that focal length can be calculated by lens makers formula which is given as:
$\dfrac{1}{f} = (\mu - 1)\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)$
Here ${R_1}$ and${R_2}$ are radii of curvature of each surface.
Now , According to the statement of equiconvex lens given in question, we have
${R_1} = {R_2} = \left| f \right| = R$
We know second radius of curvature is behind the lens , so according to coordinate system we have:
$\therefore {R_2} = - R$
Let us substitute all the value in lens makers formula , Then we get:
$\dfrac{1}{R} = (\mu - 1)\left( {\dfrac{1}{R} - \dfrac{1}{{( - R)}}} \right)$
By simplifying the above equation we get:
$\dfrac{1}{R} = (\mu - 1)\left( {\dfrac{1}{R} + \dfrac{1}{R}} \right) \\\ \Rightarrow \dfrac{1}{R} = (\mu - 1)\left( {\dfrac{2}{R}} \right) \\\ \Rightarrow (\mu - 1) = \dfrac{1}{R} \times \dfrac{R}{2} \\\ \Rightarrow (\mu - 1) = \dfrac{1}{2} \\\ \Rightarrow \mu = \dfrac{1}{2} + 1 = \dfrac{{1 + 2}}{2} = \dfrac{3}{2} \\\ \Rightarrow \mu = \dfrac{3}{2} \\\$
Therefore, the refractive index of the material of the lens is $\dfrac{3}{2}$

Note : A material's refractive index is a dimensionless number which describes how easily light passes through the given material. It is defined as the ratio of c to v where c is the vacuum velocity of light, and v is the medium phase velocity of light. Lens makers use formula from the lens supplier to create lenses with the desired focal length. Lens maker's formula is unique for all types of lens.