Question

The focal length of a thin biconvex lens is 20 cm. When an object is moved from a distance of 25 cm in front of it to 50 cm, the magnification of its image changes from ${{m}_{25}}$ to ${{m}_{50}}$. Then what is the value of the ratio $\dfrac{{{m}_{25}}}{{{m}_{50}}}$?

Answer 1

Magnification is the increase in size of an image produced by an optical system compared to its actual size. Magnification of an object from an optical lens is the ratio of distance of the image to the distance of the object as measured from the optical centre.
Use lens formula to find distance of image and use it in magnification expression.
Formula used:
Magnification formula for lens, $m=\dfrac{v}{u}$; Lens formula $\dfrac{1}{f}=\dfrac{1}{v}+\dfrac{1}{u}$

Complete answer:
Magnification is the increase in size of an image produced by an optical system compared to its actual size. In other words, it is the ratio of the height of an image produced by an optical system to the height of an object.
Magnification of an object from an optical lens is the ratio of distance of the image to the distance of the object as measured from the optical centre.
$m=\dfrac{v}{u}$
Lens formula of an optical relates its focal length, distance of object and distance of image. It is given as
$\dfrac{1}{f}=\dfrac{1}{v}+\dfrac{1}{u}$
Focal length of convex lens $f=20cm$

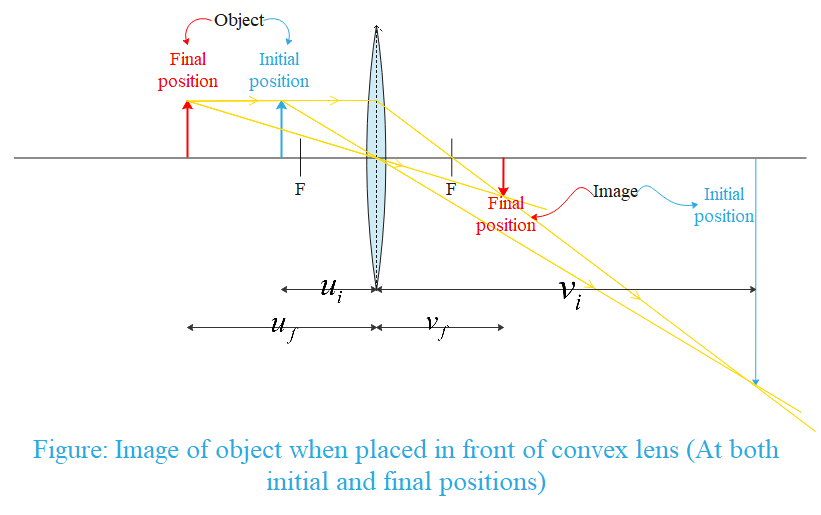
Initially the object is placed at a distance of 25 cm i.e. ${{u}_{i}}=-25cm$. Using lens formula
$\dfrac{1}{f}=\dfrac{1}{{{v}_{i}}}+\dfrac{1}{{{u}_{i}}}\Rightarrow \dfrac{1}{{{v}_{i}}}=\dfrac{1}{{{u}_{i}}}+\dfrac{1}{f}$
$\dfrac{1}{{{v}_{i}}}=\dfrac{1}{-25}-\dfrac{1}{-20}=\dfrac{1}{100}\Rightarrow {{v}_{i}}=100cm$
Finally the object is placed at a distance of 50 cm i.e. ${{u}_{i}}=-50cm$. Using lens formula as we did for obtaining ${{v}_{i}}$
${{v}_{f}}=\dfrac{100}{3}cm$
Since magnification is $m=\dfrac{v}{u}$.
$\dfrac{{{m}_{25}}}{{{m}_{50}}}=\dfrac{{{v}_{i}}/{{u}_{i}}}{{{v}_{f}}/{{u}_{f}}}=\dfrac{100/(-25)}{(100/3)/\left( -50 \right)}=6$

Note:
In mirror as well as optical lens problems, the most important thing to consider is sign conventions. Therefore, students should understand the sign conventions properly and then proceed with the solution. Diagrams are very helpful in understanding the sign conventions.
Focal length of a convex lens is always taken positively.