Question

The focal length of a convex mirror is 10cm. An object is placed before the convex mirror at 20cm distance. Then
(i) Where should be the image collected?
(ii) What are the properties of the image?

Answer 1

Hint: The lens formula can be used to calculate the distance of image from the lens from the information of focal length and position of object with respect to the lens. The properties of the image formed can be deduced by drawing a ray diagram for the problem.

Formula used:
Lens formula is given as:
$\dfrac{1}{f} = \dfrac{1}{{\text{v}}} - \dfrac{1}{u}$
where f is used to represent the focal length of the lens, while u and v represent the distance of the object and its image respectively from the lens.

Detailed step by step solution:
Convex lens is also known as the converging lens because it converges the light rays passing through the lens.
We are given that the focal length of a convex lens is given as
$f = 10cm$
An object is placed in front of this convex lens at a distance which is given as
$u = - 20cm$
Now, we can calculate the position of the image formed due to this object by using the lens formula given in the Formula used section in the following way.
$\dfrac{1}{f} = \dfrac{1}{{\text{v}}} - \dfrac{1}{u}$
Now, substituting the known values in this equation, we get
$\dfrac{1}{{10}} = \dfrac{1}{{\text{v}}} - \dfrac{1}{{ - 20}} \\\ \Rightarrow \dfrac{1}{{10}} = \dfrac{1}{{\text{v}}} + \dfrac{1}{{20}} \\\ \Rightarrow \dfrac{1}{{\text{v}}} = \dfrac{1}{{10}} - \dfrac{1}{{20}} \\\ \Rightarrow \dfrac{1}{{\text{v}}} = \dfrac{{2 - 1}}{{20}} = \dfrac{1}{{20}} \\\ \Rightarrow {\text{v }} = 20cm \\\$
This means that the image of the object is formed at a distance of 20 cm from the lens on the right side of the lens. We can find out the nature of the image formed by drawing the ray diagram as shown below:

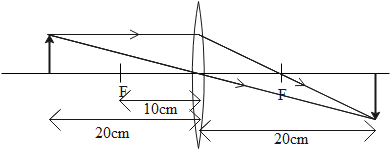
We can see from the diagram that the image formed is real image, is inverted with respect to the object and the size of the image is same as that of object which can be checked using the magnification formula which is given as
$m = \dfrac{{\text{v}}}{u} = - \dfrac{{20}}{{20}} = - 1$

Note: 1. All distances to the left of the lens are taken to be negative while all distances to the right of the lens are taken to be negative.
2. When the image of the object is formed at the same distance from the lens as that of the object, then the size of the image is also the same as that of the object.