Question

The focal length of a concave mirror is $f$ and the distance from the object to the principal focus is $x$. The ratio of the size of image to the size of object is:
(A) $\dfrac{{f + x}}{f}$
(B) $\dfrac{f}{x}$
(C) $\sqrt {\dfrac{f}{x}}$
(D) $\dfrac{{{f^2}}}{{{x^2}}}$

Answer 1

To solve this question we need to use the mirror equation. From there we can easily find the image distance, which can be put in the magnification formula to get the final answer.
Formula used: The formulas used in solving this problem are:
where $f =$focal length of the mirror, $v =$the distance of the image from the pole of the mirror and $u =$the distance of the object from the pole of the mirror
$\Rightarrow m = - \dfrac{v}{u}$, where m is the magnification

Complete step by step answer:
The mirror equation is given as
$\Rightarrow \dfrac{1}{f} = \dfrac{1}{v} + \dfrac{1}{u}$ (1)

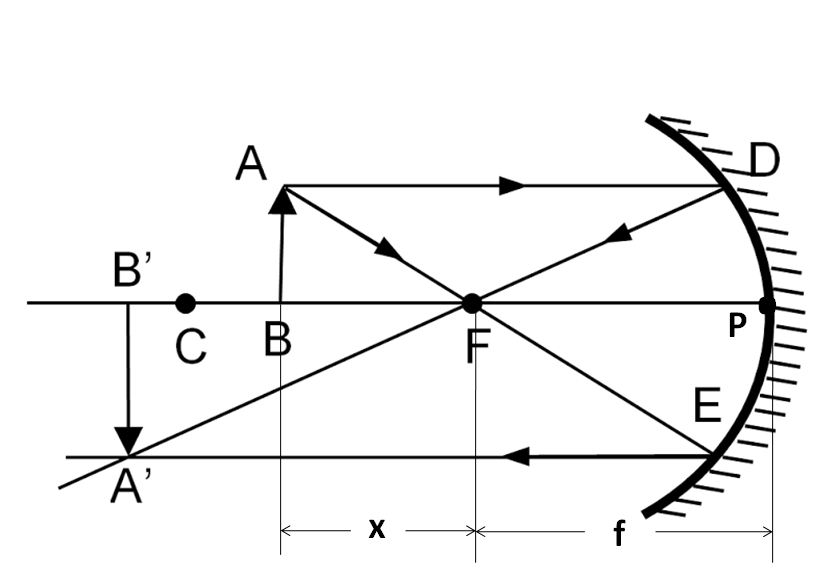
According to the question, we have our object $x$ distance from the principal focus F, as shown in the figure above.
From the above figure,
$\Rightarrow u = (f + x)$, $f = f$
As the mirror is concave, both these distances have to be taken as negative as per the Cartesian sign convention.
$\Rightarrow \therefore f = - f$and$u = - (f + x)$
Substituting these in the mirror equation (1)
$\Rightarrow - \dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{{(f + x)}}$
$\Rightarrow \dfrac{1}{v} = \dfrac{1}{{(f + x)}} - \dfrac{1}{f}$
Taking LCM
$\Rightarrow \dfrac{1}{v} = \dfrac{{f - (f + x)}}{{f(f + x)}}$
$\Rightarrow \dfrac{1}{v} = \dfrac{{ - x}}{{f(f + x)}}$
Taking reciprocal, we get
$\Rightarrow v = - \dfrac{{f(f + x)}}{x}$
We know from the magnification formula
$\Rightarrow m = - \dfrac{v}{u}$
Substituting $v = - \dfrac{{f(f + x)}}{x}$and $u = - (f + x)$
$\Rightarrow m = - \left( {\dfrac{{\dfrac{{ - f(f + x)}}{x}}}{{ - (f + x)}}} \right)$
$\Rightarrow m = - \dfrac{f}{x}$ (2)
We know that magnification is the ratio of the height of the image to the height of the object, i.e.
$\Rightarrow m = \dfrac{I}{O}$ (3)
From (2) and (3)
$\Rightarrow \dfrac{I}{O} = - \dfrac{f}{x}$
The negative sign indicates that the image formed is inverted. Ignoring the negative sign, we get
$\Rightarrow \dfrac{I}{O} = \dfrac{f}{x}$
Hence the correct answer is option (B); $\dfrac{f}{x}$.

Additional Information
We have another optical instrument in ray optics called a lens. The corresponding relation between $f,$ $v$ and $u$, called the lens formula is given by
$\Rightarrow \dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$
And the corresponding formula for the magnification is given by the relation
$\Rightarrow m = \dfrac{v}{u}$

Note:
Proper care of the sign convention is to be taken while substituting the values of $f$,$u$ or $v$ in the mirror equation. All the distances are measured from the pole of the mirror. All the distances in the direction of the incident light are taken as positive, while those opposed to the direction of incident light are taken as negative.