Question

The focal chord to ${y^2} = 16x$ is tangent to ${\left( {x - 6} \right)^2} + {y^2} = 2$, then the possible value of the slope of this chord are
\eqalign{ & 1)\left\\{ { - 1,1} \right\\} \cr & 2)\left\\{ { - 2,2} \right\\} \cr & 3)\left\\{ { - 2,\dfrac{{ - 1}}{2}} \right\\} \cr & 4)\left\\{ {2,\dfrac{{ - 1}}{2}} \right\\} \cr}

Answer 1

Hint : The given equations are of a parabola and of a circle. It is given that the focal chord of the parabola is tangent to the circle. Draw a diagram according to the given data. Then, we can find out the focus of the parabola, the radius of the circle. To find the slope, we need to find the tangent angle.

Complete step-by-step answer :
From the given data,
Equation of parabola is ${y^2} = 16x$
Equation of the circle is ${\left( {x - 6} \right)^2} + {y^2} = 2$
We know that the equation for a parabola is in the form of ${y^2} = 4ax$
Comparing the given equation with the general equation, we get
\eqalign{ & 4a = 16 \cr & \Rightarrow a = 4 \cr}
The focus of the parabola is given by $(a,0)$
Which will be $(4,0)$
It is mentioned that the focal chord of the parabola is tangent to the circle.
The equation of the circle is ${\left( {x - 6} \right)^2} + {y^2} = 2$
The general equation of the circle is given by, ${(x - h)^2} + {(y - k)^2} = {r^2}$
$h,k$ is the centre of the circle and $r$ is the radius of the circle.
Comparing the equations, we get,
Centre as $(6,0)$ and radius as $\sqrt 2$
From the derived data, we can draw the following diagram

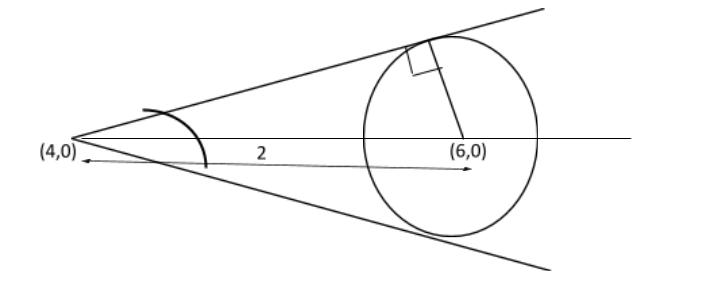
The radius is perpendicular to the tangent, we have length of tangent from $\left( {4,0} \right)$ to the circle can be $\sqrt 2$
From the diagram, we can see that
\eqalign{ & \tan \theta = \dfrac{{\sqrt 2 }}{{\sqrt 2 }} \cr & \Rightarrow \tan \theta = 1 \cr}
Now, by taking the inverse,
\eqalign{ & \theta = {\tan ^{ - 1}}(1) \cr & \theta = {45^ \circ } \cr}
Therefore, the slope of the chord is $\pm 1$.
The final answer is $\left( { - 1,1} \right)$
Hence, option (1) is the correct answer.
So, the correct answer is “Option 1”.

Note : Understand the terms chord, tangent, perpendicular clearly. Do not forget to draw the diagram, it gives us a better picture of the question. When the slope is found, it can either be positive or negative, do not ignore the signs.