Question
Question: The flux of the electric field due to charges distributed in a sphere of radius \(5\;cm\) is \(10\;V...
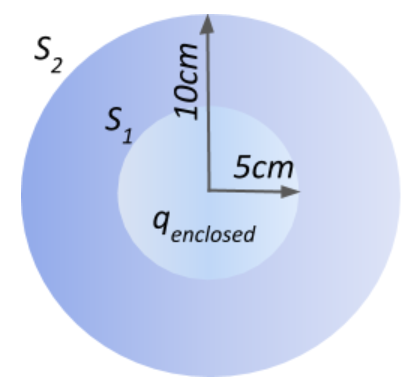
The flux of the electric field due to charges distributed in a sphere of radius 5cm is 10Vm. What will be the electric flux, through a concentric sphere of radius 10cm?
A. 20Vm
B. 30Vm
C. 5Vm
D. 10Vm
Solution
Recall the relation between the flux of the electric field and the charge enclosed in a volume by a surface. In other words, we know that the flux is directly proportional to the sum of all charges enclosed by a closed surface. Then, we know that the bigger sphere encases the smaller charge containing the sphere, so think of what charges would in turn be enclosed by the bigger sphere. Using these two statements, arrive at a conclusion that suggests an exclusive relationship between the flux and the charge enclosed, which will lead you to the solution.
Formula used: Total electric flux through a closed surface:
ϕ=ϵ0Σqenclosed, where q is the charge enclosed by the closed surface and ϵ0 is the permittivity of free space.
Complete step by step answer:
Let us begin by looking at what electric flux means.
Electric flux ϕ can be thought of as the number of electric field lines passing through a given surface area.
Now, a relation between the total flux linked with a closed surface and the charge enclosed by that surface can be established in what we call as the Gauss Law formula. It is given as:
ϕ=ϵ0Σqenclosed, where ϕ is the flux linked with the closed surface enclosing any volume V, Σqenclosed is the sum of all charges enclosed within the volume V, and ϵ0 is the electric permittivity of free space.
Now, let us slip into the context of our question.
We are given with a sphere of radius 5cm. Let the surface of this sphere be S1, and let the volume of the sphere be V in which all the charges are contained. The flux produced as a result of these enclosed charges is given as 10Vm
Now, if we have another sphere of radius 10cm built concentrically around the sphere with surface S1, the volume of the bigger sphere houses the volume of the smaller sphere. This means that the charges enclosed by surface S2 are the same as the charges enclosed by surface S1 in this particular case. From this deduction, we can thus conclude that the electric flux through the bigger sphere will be the same as the flux through the smaller sphere since both the spheres enclose the same sum of charges.
Thus, flux for the sphere with surface S2 will be 10Vm.
So, the correct answer is “Option D”.
Note: Note that the Gauss theorem gives an important corollary which states that the electric flux from any closed surface is due to the positive charges (sources) and negative charges (sinks) of the electric field enclosed by the surface. This means that no external charges contribute to the electric flux.
