Question

The figure shows two processes A and B for a gas. If $\Delta {Q_A}$ and $\Delta {Q_B}$ are the amount of heat absorbed by the system in two cases. And $\Delta {U_A}$ and $\Delta {U_B}$ are changes in internal energies, respectively, then:
(A). $\Delta {Q_A} = \Delta {Q_B};\Delta {U_A} = \Delta {U_B}$
(B). $\Delta {Q_A} > \Delta {Q_B};\Delta {U_A} = \Delta {U_B}$
(C). $\Delta {Q_A} > \Delta {Q_B};\Delta {U_A} > \Delta {U_B}$
(D). $\Delta {Q_A} < \Delta {Q_B};\Delta {U_A} < \Delta {U_B}$

Answer 1

Hint: To solve this type of problem we will use the relation between work, change in heat and change in internal energy of a system. With the help of a given curve we will solve the given problem as we know the area under the pv curve gives us the total work done of a system.

Formula used- $\Delta Q = \Delta U + w$

Complete step-by-step solution -

Where Q is heat supplied to the system, U is the change in the internal energy of the system and w is the work done by the system.

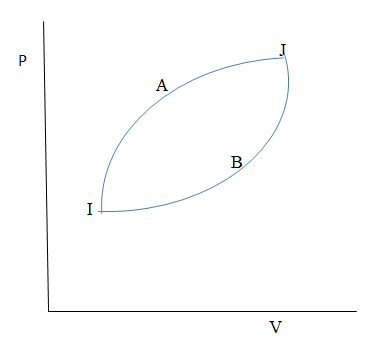
As we know that the area under the pv curve gives the total work done.
So in the above figure the area under the process A is more than the area under the process B. therefore the work done by the process A is more than the work done by the process b.
${w_A} > {w_B}$
For A system
$\Delta {Q_A} = \Delta {U_A} + {w_A}$
For B system
$\Delta {Q_B} = \Delta {U_B} + {w_B}$
And work
${w_A} > {w_B}$
Now, we will check each option one by one
First option
$\Delta {Q_A} = \Delta {Q_B};\Delta {U_A} = \Delta {U_B}$
if $\Delta {Q_A} = \Delta {Q_B}$ then, $\Delta {U_A} < \Delta {U_B}$
so the first option is wrong.
And similarly option B and C are not correct.
Now for D option
If $\Delta {Q_A} < \Delta {Q_B}$ then, $\Delta {U_A} < \Delta {U_B}$
So, the correct option is D.

Note- In the given equation $\Delta Q = \Delta U + w$ , work may be positive or negative depending on the volume of the system. If the volume increases then the work will be positive and if the volume of the system decreases work will be negative. And if volume remains constant then work is zero and heat supplied is equal to the changes in internal energy.