Question
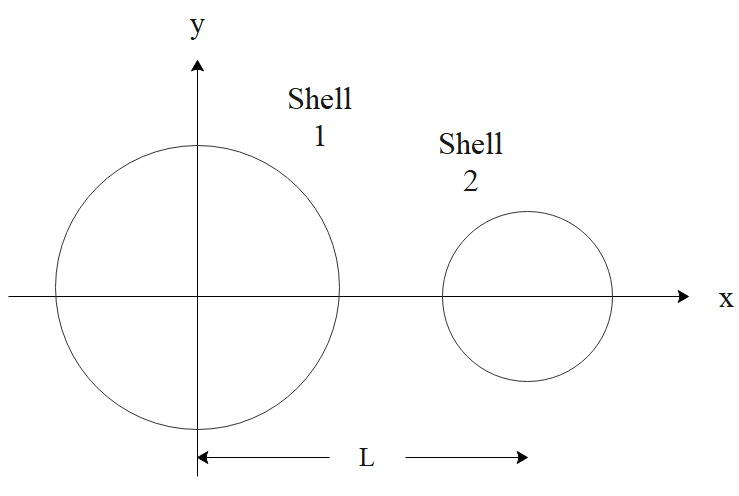
Question: The figure shows two nonconducting spherical shells fixed in place. Shell 1 has a uniform surface ch...
The figure shows two nonconducting spherical shells fixed in place. Shell 1 has a uniform surface charge density 6.0μC/m2 on its outer surface and radius 43.0cm; shell 2 has a uniform surface charge density 4.0μC/m2 on its outer surface and radius 2.0cm; the shell centres are separated by L=10cm. In unit-vector notation, what is the net electric field at x=2.0cm?
Solution
We know that electric field, an electric property associated with each point in space when charge is present in any form. The magnitude and direction of the electric field are expressed by the value of E, called electric field strength or electric field intensity or simply the electric field. The space around an electric charge in which its influence can be felt is known as the electric field. The electric field Intensity at a point is the force experienced by a unit positive charge placed at that point. Electric Field Intensity is a vector quantity.
Complete step by step answer
We know that the electric field is defined as the electric force per unit charge. The direction of the field is taken to be the direction of the force it would exert on a positive test charge. The electric field is radially outward from a positive charge and radially in toward a negative point charge.
Electric field is not negative. It is a vector and thus has negative and positive directions. An electron being negatively charged experiences a force against the direction of the field. For a positive charge, the force is along the field.
We note that only the smaller shell contributes a (nonzero) field at the designated point since the point is inside the radius of the large sphere (and E=0 inside of a spherical charge) and the field
points toward the - x direction. Thus, with R=0.020m (the radius of the smaller shell), L=0.10m and x=0.020m, we obtain
E=E(j)=−4πer2qj=−4πϵ0(L−x)24πR2σ2j= −ϵ0(L−x)2R2σ2j
After we put the values, we get that:
=−(8.85×10−12C2/N⋅m)(0.10m−0.020m)2(0.020m)2(4.0×10−6C/m2)j
After the evaluation we get: (−2.8×104N/C)j
Note: We know that electric fields (e-fields) are an important tool in understanding how electricity begins and continues to flow. The electric fields of single charges. A negative charge has an inward electric field because it attracts positive charges. The positive charge has an outward electric field, pushing away like charges. Electric field is defined as the electric force per unit charge. The direction of the field is taken to be the direction of the force it would exert on a positive test charge. The electric field is radially outward from a positive charge and radially in toward a negative point charge. Electric field lines cannot cross. This is because they are, by definition, a line of constant potential. The equipotential at a given point in space can only have a single value. If lines for two different values of the potential were to cross, then they would no longer represent equipotential lines.
