Question

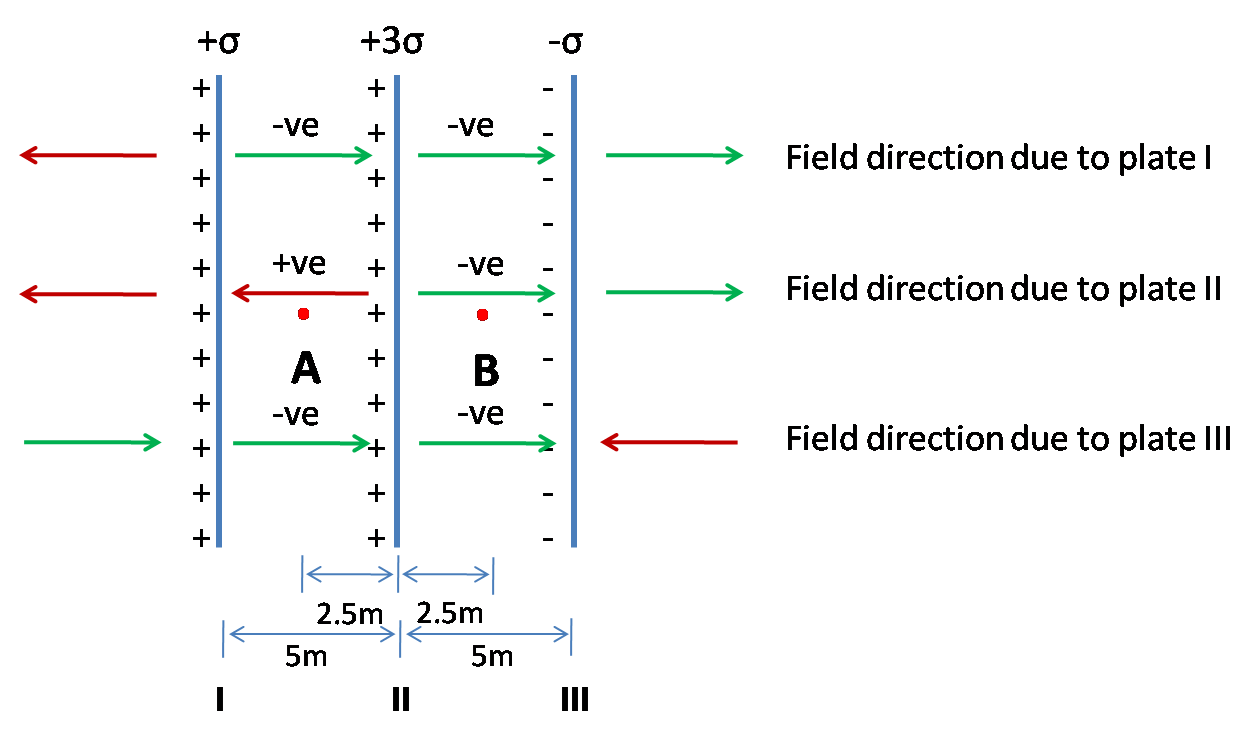
The figure shows three infinite non-conducting plates of charge perpendicular to the plane of the paper with charge per unit area $+ \sigma , + 3\sigma$ and$- \sigma$. The ratio of the net electric field at the point A to the point B is$1/x$ . Find x.

Answer 1

To solve this problem, first we need to find out the net electric fields at the points A and B. For that, we may use the equation for the electric field at a point near to an infinite non-conducting plate having a given charge density, $E = \dfrac{\sigma }{{2\varepsilon 0}}$. The net electric fields at both the points can be calculated by adding the individual electric fields due to each of the infinite non-conducting plates.

Formula used: Here we use the equation which can be derived from Gauss law: $E = \dfrac{\sigma }{{2\varepsilon 0}}$where $E$ is the electric field, $\sigma$ is the surface charge density or charge per unit area of the infinite non-conducting plate, and $\varepsilon 0$ is the permittivity of free space.

Complete step-by-step answer:
As we all can understand from the figure, it is clear that the net electric field at point A has contributions of the fields due to the plates I, II and III. The figure clearly describes that the surface charge densities of the plates I, II and III are $+ \sigma , + 3\sigma$and $- \sigma$ respectively. Now, the electric field at point A due to the plate I would be:
$EA\left( I \right) = \dfrac{{ - \sigma }}{{2\varepsilon 0}}$
Similarly, the electric field at A due to the plates II and II are:
$$
EA\left( {II} \right) = \dfrac{{3\sigma }}{{2\varepsilon 0}} \\
EA\left( {III} \right) = \dfrac{{ - \sigma }}{{2\varepsilon 0}} \\

respectively. Now, the net electric field at A is given by: $$ EA = EA\left( I \right) + EA\left( {II} \right) + EA\left( {III} \right) \\\ \Rightarrow EA = \dfrac{{ - \sigma }}{{2\varepsilon 0}} + \dfrac{{3\sigma }}{{2\varepsilon 0}} + \dfrac{{ - \sigma }}{{2\varepsilon 0}} = \dfrac{\sigma }{{2\varepsilon 0}} \\\

Similarly the electric fields at point B due to the three plates are given by:

 $$  

EB\left( I \right) = \dfrac{{ - \sigma }}{{2\varepsilon 0}} \\
EB\left( {II} \right) = \dfrac{{ - 3\sigma }}{{2\varepsilon 0}}and \\
EB\left( {III} \right) = \dfrac{{ - \sigma }}{{2\varepsilon 0}} \\

Thus, the net electric field at the point B can be estimated as: $$ EB = EB\left( I \right) + EB\left( {II} \right) + EB\left( {III} \right) \\\ \Rightarrow EA = \dfrac{{ - \sigma }}{{2\varepsilon 0}} + \dfrac{{ - 3\sigma }}{{2\varepsilon 0}} + \dfrac{{ - \sigma }}{{2\varepsilon 0}} = \dfrac{{ - 5\sigma }}{{2\varepsilon 0}} \\\

Finally, the ratio of the net electric field at point A to that at point B

 $$\left| {\dfrac{{EA}}{{EB}}} \right| = \dfrac{\sigma }{{2\varepsilon 0}} \div \dfrac{{5\sigma }}{{2\varepsilon 0}} = \dfrac{\sigma }{{2\varepsilon 0}} \times \dfrac{{2\varepsilon 0}}{{5\sigma }} = \dfrac{1}{5}$$   

So, as we found that the ratio of the net electric fields at both the points is $\dfrac{1}{5}$, the value of $x = 5$.

Note: When we are performing the calculation of the individual electric fields at both the points due to each of the non-conducting plates, we may sometimes end up in making the mistake of putting a wrong polarity. So, it is important to keep in mind that the electric field lines travel away from the positive plates while they travel towards the negative plates, shown in the illustration below. If we give the polarity of the field at a point depending on the direction of the field lines and then do the summation, the problem can be solved very easily.