Question

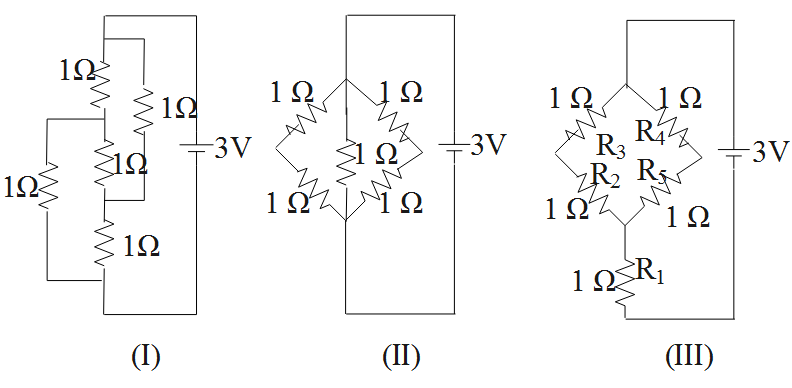
The figure shows three circuits I, II and III which are connected to a 3 V battery. If the powers dissipated by the configurations I, II and III are ${{P}_{1}},{{P}_{2}}$and ${{P}_{3}}$respectively, then:

& A.\,{{P}_{1}}>{{P}_{3}}>{{P}_{2}} \\\ & B.\,{{P}_{2}}>{{P}_{1}}>{{P}_{3}} \\\ & C.\,{{P}_{1}}>{{P}_{2}}>{{P}_{3}} \\\ & D.\,{{P}_{3}}>{{P}_{2}}>{{P}_{1}} \\\ \end{aligned}$$

Answer 1

The power equals the square of the voltage by the resistance. Thus, the circuit with the maximum resistance will have the least power dissipated, similarly, the circuit with the minimum resistance will have the highest power dissipated. The value of the voltage is given for creating confusion.

Formula used:
$P=\dfrac{{{V}^{2}}}{R}$

Complete step-by-step answer:
From the given information, we have three circuits with a different number of resistors in them.
Firstly, we have to compute the value of the equivalent resistance of all the three circuits.
Consider the first circuit.

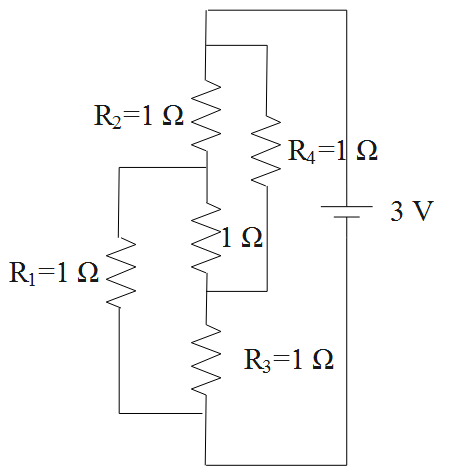
The above circuit represents the balanced Wheatstone bridge with centre resistance to be zero.
The equivalent resistance is,

& {{R}_{1}}+{{R}_{2}}=1+1=2\Omega \\\ & {{R}_{3}}+{{R}_{4}}=1+1=2\Omega \\\ & {{R}_{eq}}=\dfrac{2}{2}=1\Omega \\\ \end{aligned}$$ The power is, $$\begin{aligned} & {{P}_{1}}=\dfrac{{{V}^{2}}}{R} \\\ & \Rightarrow {{P}_{1}}=\dfrac{{{3}^{2}}}{1} \\\ & \therefore {{P}_{1}}=9\,W \\\ \end{aligned}$$ Consider the second circuit.  The equivalent resistance is, $$\begin{aligned} & {{R}_{5}}={{R}_{1}}+{{R}_{2}}=1+1=2\Omega \\\ & {{R}_{6}}={{R}_{3}}+{{R}_{4}}=1+1=2\Omega \\\ & {{R}_{7}}=\dfrac{{{R}_{5}}\times {{R}_{6}}}{{{R}_{5}}+{{R}_{6}}}=\dfrac{2\times 2}{2+2}=1\Omega \\\ & {{R}_{eq}}=\dfrac{{{R}_{5}}\times {{R}_{7}}}{{{R}_{5}}+{{R}_{7}}}=\dfrac{1}{2}\Omega \\\ \end{aligned}$$ The power is, $$\begin{aligned} & {{P}_{2}}=\dfrac{{{V}^{2}}}{R} \\\ & \Rightarrow {{P}_{2}}=\dfrac{{{3}^{2}}}{{}^{1}/{}_{2}} \\\ & \therefore {{P}_{2}}=18\,W \\\ \end{aligned}$$ Consider the second circuit.  The equivalent resistance is, $$\begin{aligned} & {{R}_{6}}={{R}_{2}}+{{R}_{3}}=1+1=2\Omega \\\ & {{R}_{7}}={{R}_{4}}+{{R}_{5}}=1+1=2\Omega \\\ & {{R}_{8}}=\dfrac{{{R}_{7}}\times {{R}_{6}}}{{{R}_{7}}+{{R}_{6}}}=\dfrac{2\times 2}{2+2}=1\Omega \\\ & {{R}_{eq}}={{R}_{1}}+{{R}_{8}}=1+1=2\Omega \\\ \end{aligned}$$ The power is, $$\begin{aligned} & {{P}_{3}}=\dfrac{{{V}^{2}}}{R} \\\ & \Rightarrow {{P}_{3}}=\dfrac{{{3}^{2}}}{2} \\\ & \therefore {{P}_{3}}=4.5\,W \\\ \end{aligned}$$ Now we will compare the values of the powers of all the three circuits. So, we have, $$\begin{aligned} & {{P}_{1}}=9\,W \\\ & {{P}_{2}}=18\,W \\\ & {{P}_{3}}=4.5\,W \\\ & 18>9>4.5 \\\ & \therefore {{P}_{2}}>{{P}_{1}}>{{P}_{3}} \\\ \end{aligned}$$ Even without using the voltage value, we can solve this problem, as, the power and the resistance are inversely proportional to each other. Thus, the circuit with the highest value of the resistance will have the least power dissipation and the circuit with the lowest value of the resistance will have the highest power dissipation. The relation between the power and resistance is given as follows. $$\begin{aligned} & P=\dfrac{{{V}^{2}}}{R} \\\ & \therefore P\propto \dfrac{1}{R} \\\ \end{aligned}$$ $$\therefore $$ The power dissipated by circuit 2 is greater than the power dissipated by the circuit 1 and this power dissipated greater than the power dissipated by the circuit 3, thus, option (B) is correct. **So, the correct answer is “Option B”.** **Note:** In this question, the value of the voltage is given. Even they can give the value of the current. In such a case, power equals the product of the square of the current times the resistance of the circuit. If the values of voltage and current are given, then, the power is the product of the voltage and the current.