Question

The figure shows the position time (x-t) graph of one-dimensional motion of a body of mass 0.4kg. The magnitude of each impulse is

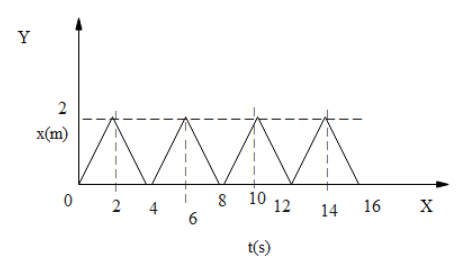
$\begin{aligned} & (A)0.4Ns \\\ & (B)0.8Ns \\\ & (C)1.6Ns \\\ & (D).2Ns \\\ \end{aligned}$

Answer 1

Impulse is the change in momentum of a body. Thus first calculate the change in momentum. The momentum can be calculated using mass and velocity. Since here we want to find the change in momentum, it will be the product of mass and change in velocity. Thus calculate initial and final velocities and calculate its difference. Then we get the change in velocity. Using this, calculate the change in momentum which is known as the impulse.

Complete answer:
The graph shows a straight line, so the motion here is a uniform motion. Because of impulse, direction of velocity changes. The velocity here is the slope of the graph.
The change in momentum is given by,
$\vartriangle p=m\vartriangle v$ ……………..(1)
Thus change in velocity is,
$\Rightarrow \vartriangle v={{v}_{1}}-{{v}_{2}}$
Here velocity means the slope of the x-t graph. Therefore,
$\Rightarrow v=\dfrac{dx}{dt}=$ slope of x-t
$\Rightarrow {{v}_{1}}=\left( \dfrac{2-0}{2-0} \right)=1m/s$
$\Rightarrow {{v}_{2}}=\left( \dfrac{0-2}{4-2} \right)=-1m/s$
Then substituting the value of mass and change in velocity in equation (1) we get,
$\Rightarrow m\times ({{v}_{1}}-{{v}_{2)}}$ $=m\times \left[ \left( \dfrac{2-0}{2-0} \right)-\left( \dfrac{0-2}{4-2} \right) \right]$
Thus change in momentum becomes,
$\Rightarrow \vartriangle p=0.4\times \left( 1-\left( -1 \right) \right)=0.4\times 2=0.8Ns$
And we know that the impulse is the change in momentum of a body.
Thus, impulse $=0.8Ns$

Hence option (B) is correct.

Note:
Impulse is the change in momentum of a body. The SI unit of momentum is Ns. Impulse means a fast acting force or impact. The impulse experienced by the thing equals the change in momentum of another object. In equation form, $F\times t=m\times \vartriangle v$. In a collision, objects experience an impulse; the impulse causes and is adequate to the change in momentum. In a collision, the impulse experienced by an object is always similar to the momentum change.