Question
Question: The figure shows the graph of deviation \('\delta '\) versus the angle of incidence \(\varphi \) for...
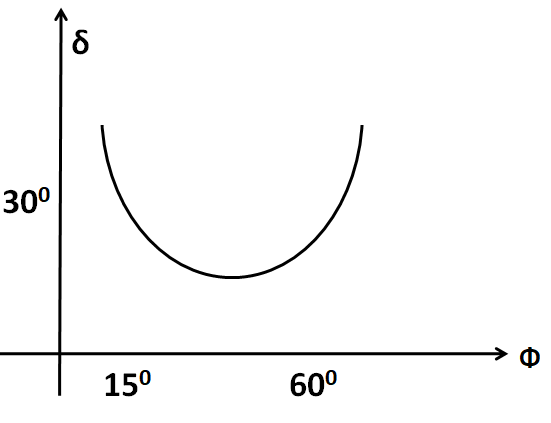
The figure shows the graph of deviation ′δ′ versus the angle of incidence φ for a light ray striking a prism. The angle of the prism is:
A. 30∘
B. 45∘
C. 60∘
D. 75∘
Solution
To solve this question, we need to use the formula of the angle of deviation for a light ray incident on a prism. Substituting the values of the two angles of incidence for the given value of the angle of deviation in that formula, we will get the required value of the angle of prism.
Formula used: The formula used to solve this question is given by
δ=i+e−A, here δ is the angle of deviation for a light ray incident on a prism of angle A at an angle of incidence of i, which leaves the prism with an angle of emergence of e.
Complete step by step answer: We know that the angle of deviation for a ray of light passing through a prism is given by the formula
δ=i+e−A.
According to the figure given in the question, for the values of the angle of incidence of the ray of light equal to 15∘ and 60∘, we have the same angle of deviation equal to 30∘. Therefore, we can take one of the two angles like the angle of incidence, and the other to be equal to the angle of emergence.
Therefore, on substituting i=15∘, e=60∘, and δ=30∘ in the above formula, we get
30∘=15∘+60∘−A
⇒A=15∘+60∘−30∘
On solving, we finally get the value of the angle of prism as
A=45∘
Thus, the value of the angle of prism is equal to 45∘.
Hence, the correct answer is option B.
Note: Do not be confused as to how could we take the angle of emergence to be equal to the angle of incidence. We can clearly see that the formula for the angle of deviation is symmetric with respect to the angle of incidence and the angle of emergence. This means that these values are exchangeable. In the other words, if the path of the emergent ray is reversed so that it is incident on the other face of the prism at the angle of emergence, then it would emerge from the first face of the prism making an angle equal to the angle of incidence.
