Question

The figure shows the graph of a current in a discharging circuit of a capacitor through a resistor of resistance 10 ohm:

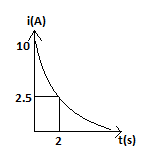
A. The initial potential difference across the capacitor is 100V.
B. The capacitance of the capacitor is $\dfrac{1}{{10\ln 2}}$ F.
C. The total heat produced in the circuit will be $\dfrac{{500}}{{\ln 2}}$ J.
D. All of the above.

Answer 1

For solving the problem we will use the transient behaviour of the capacitor that the capacitor will have initial current and initial voltage zero after charging the capacitor will have zero current (as shown the decaying current of the graph) and maximum voltage.

Complete answer:
Let’s check each option one by one in order to mark the correct option:
A) Initial potential difference of the capacitor is 100V.Initial current of the capacitor is 10 as per graph and the resistance is 10 ohm therefore voltage will be V = I$\times$ R. Multiplication of current and resistance will give us; 10 $\times$ 10 =100 V.
B) Equation of current at time t is:
$i(t) = {i_0}{e^{ - \dfrac{t}{\tau }}}$ (Where i0 is the initial current t is the time and $\tau$is the time constant = RC).
i =2.5 at t = 2 from graph. Substituting the values of i and t>
$\Rightarrow 2.5 = 10{e^{ - \dfrac{2}{{10C}}}} \\\ \Rightarrow \dfrac{{2.5}}{{10}} = {e^{ - \dfrac{2}{{10C}}}} \\\$
Now we will remove the exponential term from both the sides of the equation by taking natural log.
$\Rightarrow \ln .25 = \dfrac{{ - 2}}{{10C}} \\\ \Rightarrow - 1.3863 = \dfrac{{ - 2}}{{10C}} \\\$ (ln.25 have value -1.3863)
$\Rightarrow \dfrac{2}{{13.863}} = C \\\ \Rightarrow C = 0.1443F \\\$ (Getting value of C from this equation)

Value of $\dfrac{1}{{10\ln 2}}$is also 0.1443 F.
C) Total heat produced in the circuit means energy.
Energy of capacitor is given by $\dfrac{1}{2}C{V^2}$
$\Rightarrow \dfrac{1}{2} \times 0.1443 \times {(100)^2} \\\ \Rightarrow 0.5 \times 0.1443 \times 10000 \\\ \Rightarrow 721.500J \\\$ (Substituting all the values in the Formula used:)

Value of $\dfrac{{500}}{{\ln 2}}$ J. Is also equal to 721.500J

Therefore, option D is correct.

Note:
As the capacitor shows the transient behaviour, in the similar way the inductor too shows the transient behaviour. At the initial stage the inductor has zero current value and has voltage magnitude but at steady state voltage slows down to zero and current reaches a maximum level.