Question

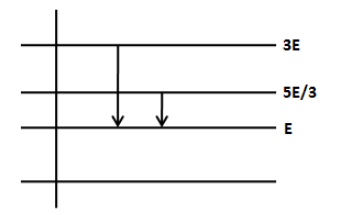
The figure shows the energy level of a certain atom. When the electron de excites from 3E to E, an electromagnetic wave of wavelength $\lambda$ is emitted. What is the wavelength of the electromagnetic wave when the electron de excites from $\dfrac{{5E}}{3}$ to E?

A. $3\lambda$
B. $2\lambda$
C. $5\lambda$
D. $\dfrac{{3\lambda }}{5}$

Answer 1

When the electron undergoes transition from higher energy level to the lower energy level, the electromagnetic radiation in the form of photon is emitted. The energy of this photon is equal to the energy difference between the two levels. Use the formula for energy of the photon in terms of the wavelength of the photon.

Formula used:
The energy of the photon is, $E = \dfrac{{hc}}{\lambda }$
Here, h is the Planck’s constant, c is the speed of light and $\lambda$ is the wavelength of the photon.

Complete step by step answer:
We know that when the electron de excites from higher level to the lower level, it emits a photon with energy equal to difference in the energy levels. Let’s calculate the energy difference when the electron de excites from 3E to E as follows,
$3E - E = 2E$

The energy of the photon is equal to the energy difference of the energy levels. Therefore, we can express the energy of the photon as,
$2E = \dfrac{{hc}}{\lambda }$ …… (1)
Here, h is the Planck’s constant, c is the speed of light and $\lambda$ is the wavelength of the photon.

The energy difference in the second transition from $\dfrac{{5E}}{3}$ to E is,
$\dfrac{{5E}}{3} - E = \dfrac{{2E}}{3}$

We know that the photon emitted in this transition has the energy equal to $\dfrac{{3E}}{2}$. Therefore, let’s express the energy of the photon as,
$\dfrac{{2E}}{3} = \dfrac{{hc}}{{{\lambda _1}}}$ …… (2)
Here, ${\lambda _1}$ is the wavelength of the electromagnetic wave in this transition.

Dividing equation (2) by equation (1), we get,
$\dfrac{{\dfrac{{2E}}{3}}}{{2E}} = \dfrac{{\dfrac{{hc}}{{{\lambda _1}}}}}{{\dfrac{{hc}}{\lambda }}}$
$\Rightarrow \dfrac{1}{3} = \dfrac{\lambda }{{{\lambda _1}}}$
$\therefore {\lambda _1} = 3\lambda$

So, the correct answer is option A.

Note: Since the Planck’s constant and the speed of light are constant, the wavelength of the electromagnetic wave only depends on the energy difference between the two energy levels. The transition of electrons have the rules to follow, the electron does not undergo transition to every lower energy level.