Question

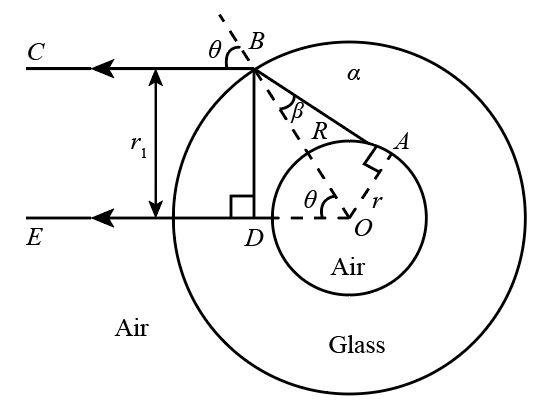
The figure shows the cross section of a hollow glass tube of internal radius $r$ and external radius $R$ and index of refraction $n$. For two rays DE and ABC (in which the DE lies on ODE and DE is parallel to BC), the separation ${r_1}$ will be:

A) ${r_1} = \left( {n - 1} \right)R$
B) ${r_1} = {n^2}R$
C) ${r_1} = nr$
D) ${r_1} = {n^2}r$

Answer 1

The above problem can be solved by applying the laws of optics and basic geometry. Find the relation between the internal radius of glass tube, external radius of glass tube and index of refraction by using the geometry. Eliminate the angles to obtain the required formula.

Complete step by step answer:
Given: The internal radius of the glass tube is $r$, external radius of the glass tube is $R$, separation of the rays is ${r_1}$ and index of refraction is $n$.
Draw the normal line from point B to the line ED. Let the angle $\angle BOD$ of the triangle BOD is $\phi$ and the angle $\angle ABO$ is $\beta$.
The diagram of the refraction of the light from glass tube is given below:

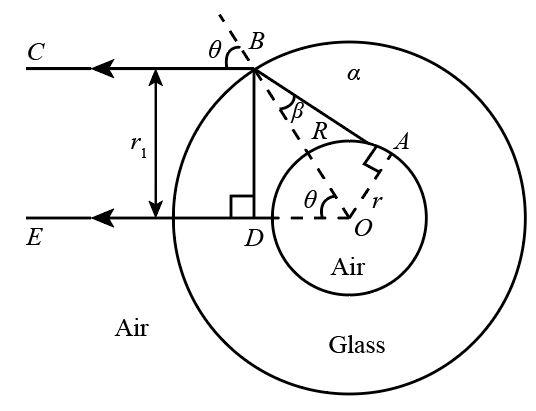
Find the sine angle of the angle $\angle BOD$ from the triangle BOD as:
$\sin \phi = \dfrac{{{r_1}}}{R}$
Find the sine angle of the angle $\angle ABO$ from the triangle ABO as:
$\sin \beta = \dfrac{r}{R}$
Apply Snell's law to find the index of refraction of the glass.
${n_a}\sin \phi = n\sin \beta ......\left( 1 \right)$
Here, ${n_a}$ is the index of refraction of the air and its value is 1.
Substitute 1 for ${n_a}$in the expression to find the value of the index of refraction of the glass.
$\left( 1 \right)\sin \phi = n\sin \beta$
$\sin \phi = n\sin \beta$
$n = \dfrac{{\sin \phi }}{{\sin \beta }}......\left( 2 \right)$
Substitute all the values in the expression (2) to find the required formula.
$n = \dfrac{{\left( {\dfrac{{{r_1}}}{R}} \right)}}{{\left( {\dfrac{r}{R}} \right)}}$
$n = \dfrac{{{r_1}}}{r}$
${r_1} = nr$

Thus, the separation between the rays is equal to the product of index of refraction of glass and internal radius of the glass tube and the option (C) is the correct answer.

Note: Be careful in calculating the angle of the refraction and applying the Snell’s law. The normal line is drawn to form the triangle BOD, so that we can find the angle BOD.