Question

The figure shows how the stream of water emerging from a faucet necks down as it falls. The area changes from ${A_0}$ to $A$ through a fall of $h$ . Find the rate at which the water flows from the tap.

Answer 1

We observe that the stream of water gets narrower as it emerges from the tap. The amount of water flowing through a cross-section of the stream of water per unit time at any point will remain constant. The amount of water flowing through the stream depends on the area of cross-section of the stream and the speed of the flow. This gives rise to the continuity equation. The energy of the stream of water remains constant.

Formulas used:
-The continuity equation for the steady flow of a fluid is given by, ${\rho _1}{A_1}{v_1} = {\rho _2}{A_2}{v_2}$ where ${\rho _1}$ , ${A_1}$ and ${v_1}$ are the density, cross-sectional area and velocity of the fluid respectively at the one point of the flow and ${\rho _2}$ , ${A_2}$ and ${v_2}$ are the density, cross-sectional area and velocity of the fluid respectively at another point in the flow.
-The change in potential energy per unit volume at height $h$ is given by, $\Delta U = \rho gh$ where $\rho$ is the density of the fluid and $g$ is the acceleration due to gravity.
-The change in kinetic energy per unit volume for a stream of water is given by, $\Delta K = \dfrac{1}{2}\left( {{v_2}^2 - {v_1}^2} \right)$ where ${v_2}$ and ${v_1}$ are the velocities of the flow at points 2 and 1 respectively.

Complete step by step answer.
Step 1: Sketch the stream of water emerging from the tap with its parameters.

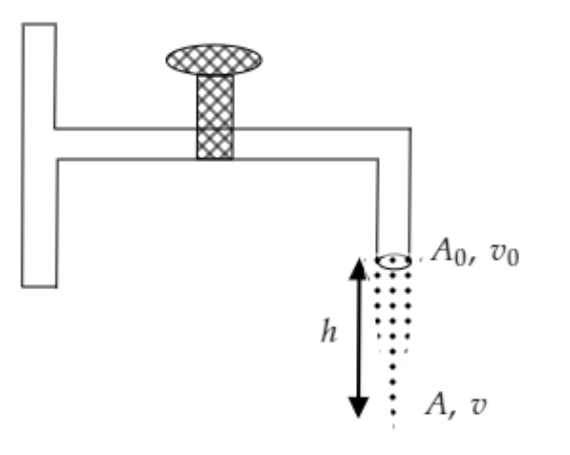
In the above figure, the area of cross-section of the stream at the opening of the tap is ${A_0}$ and at a height $h$ from the opening it is $A$ .
Also, the velocities of the flow at the opening of the tap is ${v_0}$ . The velocity of the water at a point at a distance of $h$from the opening of the tap is $v$ .
Step 2: Express the continuity equation for the flow of water from the tap.
The continuity equation for water flowing through a tap is given by, ${A_0}{v_0} = Av$ ------- (1)
where ${A_0}$ and ${v_0}$ are the cross-sectional area and velocity of the stream respectively at the opening of the tap while $A$ and $v$ are the cross-sectional area and velocity of the stream respectively at a height $h$ from the opening.
Step 3: Express the relation for the velocity of the liquid through a fall of height $h$ .
Since energy is constant, the change in potential energy per unit volume at a height $h$ from the ground is equal to the change in kinetic energy per unit volume of the stream of water.
i.e., $\Delta U = \Delta K$ or $\rho gh = \dfrac{1}{2}\left( {{v^2} - {v_0}^2} \right)$ --------- (2)
On rearranging equation (2) we get, ${v^2} = {v_0}^2 + 2gh$ --------- (3)
Step 4: Using equations (1) and (3) obtain a relation for the rate at which the water flows from the tap ${v_0}$ .
Equation (1) gives ${A_0}{v_0} = Av$ and equation (3) gives ${v^2} = {v_0}^2 + 2gh$ .
On squaring equation (1) it becomes ${A_0}^2{v_0}^2 = {A^2}{v^2}$ -------- (4)
Substituting equation (3) in (4) we get, ${A_0}^2{v_0}^2 = {A^2}\left( {{v_0}^2 + 2gh} \right)$
On expanding the bracket and grouping similar terms we get, ${v_0}^2\left( {{A_0}^2 - {A^2}} \right) = {A^2}2gh$ or ${v_0}^2 = \dfrac{{{A^2}2gh}}{{\left( {{A_0}^2 - {A^2}} \right)}}$
Taking the square root of the above equation we get, ${v_0} = \sqrt {\dfrac{{{A^2}2gh}}{{{A_0}^2 - {A^2}}}}$
So the rate at which the water flows from the tap is ${v_0} = \sqrt {\dfrac{{{A^2}2gh}}{{{A_0}^2 - {A^2}}}}$

Note: Here, a transfer of energy takes place i.e., the potential energy of the water gets converted to kinetic energy. The density of the water remains the same so we neglect the density term $\rho$ while writing the equation of continuity for the flow of water as equation (1).