Question

The figure shows an insulated cylinder divided into three parts $A$, $B$ and $C$. Piston I and II are connected by a rigid rod and can move without friction inside the cylinder. Piston I is perfectly conducting while piston II is perfectly insulating. The initial state of gas $(\gamma=1.5)$ present in each compartment A, B and $C$ is as shown. Now, compartment A is slowly given heat through a heater $\mathrm{H}$ such that the final volume of $\mathrm{C}$ becomes $\dfrac{4 V_{0}}{9} .$ Assume the gas to be ideal and find the heat supplied by the heater.

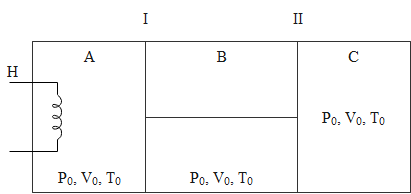
(A) $18 P_{o} V_{o}$
(B) $12 P_{o} V_{o}$
(C) $9 P_{o} V_{o}$
(D) $25 P_{o} V_{o}$

Answer 1

Hint First we need to apply the heat supply equation to determine the heat change in case of each compartment. Then equating the temperature and pressure, we will get the heat supplied by the heater.

Complete step by step answer:
We can know the heat supplied from the equation,
$\Rightarrow \Delta \mathrm{Q}=\Delta \mathrm{U}+\Delta \mathrm{W}$
$\Rightarrow \Delta \mathrm{U}=\Delta \mathrm{U}_{\mathrm{A}}+\Delta \mathrm{U}_{\mathrm{B}}+0 \quad$
We find that there is no heat change in case of compartment C
$\Rightarrow \Delta \mathrm{W}=\Delta \mathrm{W}_{\mathrm{A}}+0+\Delta \mathrm{W}_{\mathrm{C}} \quad$
We find that there is no change in volume in case of compartment B hence work done = 0
The initial conditions are assumed as
$\Rightarrow \mathrm{P}_{\mathrm{o}}$ for Pressure
$\Rightarrow \mathrm{V}_{\mathrm{o}}$for Volume
$\Rightarrow \mathrm{T}_{\mathrm{o}}$for Temperature
The final conditions in respective compartments:
In Compartment C
$\Rightarrow \mathrm{PV}^{\gamma}=\mathrm{PV}^{\gamma}=\mathrm{P} \times\left(\dfrac{4 \mathrm{V}_{0}}{9}\right)^{1.5}=\mathrm{P}_{\mathrm{o}} \mathrm{V}_{\mathrm{o}}^{1.5}$
$\Rightarrow P=\dfrac{27 P_{0}}{8}$
$\Rightarrow \dfrac{\mathrm{P}_{\mathrm{o}} \mathrm{V}_{\mathrm{o}}}{\mathrm{T}_{\mathrm{o}}}=\dfrac{\dfrac{27 \mathrm{P}_{\mathrm{o}}}{8} \times \dfrac{4 \mathrm{V}_{\mathrm{o}}}{9}}{\mathrm{T}}$
$\Rightarrow \mathrm{T}=\dfrac{3 \mathrm{T}_{\mathrm{o}}}{2}$
In Compartment A
$\Rightarrow \mathrm{P}=\dfrac{27 \mathrm{P}_{\mathrm{o}}}{8}$
For pistons to come at rest both compartment A and C have to have the same pressure.
$\Rightarrow \dfrac{\mathrm{P}_{\mathrm{o}} \mathrm{V}_{\mathrm{o}}}{\mathrm{T}_{\mathrm{o}}}=\dfrac{\dfrac{27 \mathrm{P}_{\mathrm{o}}}{8} \times\left(\mathrm{V}_{\mathrm{o}}+\dfrac{5 \mathrm{V}_{\mathrm{o}}}{9}\right)}{\mathrm{T}}$
$\Rightarrow \mathrm{T}=\dfrac{21 \mathrm{T}_{\mathrm{o}}}{4}$
In Compartment B
$\Rightarrow \mathrm{T}=\dfrac{21 \mathrm{T}_{\mathrm{o}}}{4}$
We know that the temperature of both compartment A and compartment B should be the same at equilibrium. Therefore,
$\Rightarrow \dfrac{\mathrm{P}_{\mathrm{o}} \mathrm{V}_{\mathrm{o}}}{\mathrm{T}_{\mathrm{o}}}=\dfrac{\mathrm{P} \times \mathrm{V}_{\mathrm{o}}}{\dfrac{21 \mathrm{T}_{\mathrm{o}}}{4}}$
$\Rightarrow P=\dfrac{21 P_{0}}{4}$
$\Rightarrow \gamma=\dfrac{\mathrm{C}_{\mathrm{p}}}{\mathrm{C}_{\mathrm{v}}}=\dfrac{\mathrm{f}+2}{\mathrm{f}}$
$\Rightarrow \mathrm{f}=4$
$\Rightarrow \mathrm{C}_{\mathrm{v}}=\dfrac{\mathrm{fR}}{2}=2 \mathrm{R}$
$\Rightarrow \Delta \mathrm{U}_{\mathrm{A}}=\Delta \mathrm{U}_{\mathrm{B}}$
$\Rightarrow \Delta \mathrm{U}_{\mathrm{A}}=\mathrm{n} \mathrm{C}_{\mathrm{v}} \Delta \mathrm{T}$
$\Rightarrow \Delta \mathrm{U}_{\mathrm{A}}=\dfrac{\mathrm{P}_{0} \mathrm{V}_{\mathrm{o}}}{\mathrm{RT}_{\mathrm{o}}} \times \mathrm{C}_{\mathrm{v}}\left(\dfrac{21 \mathrm{T}_{\mathrm{o}}}{4}-\mathrm{T}_{\mathrm{o}}\right)=\dfrac{\mathrm{P}_{\mathrm{o}} \mathrm{V}_{\mathrm{o}}}{\mathrm{RT}_{\mathrm{o}}} \times 2 \mathrm{R} \times \dfrac{17 \mathrm{T}_{\mathrm{o}}}{4}=\dfrac{17 \mathrm{P}_{\mathrm{o}} \mathrm{V}_{\mathrm{o}}}{2}$
$\Rightarrow \Delta \mathrm{W}_{\mathrm{A}}=-\Delta \mathrm{W}_{\mathrm{C}}$
as the gas in chamber A is working on chamber C
$\Rightarrow \Delta \mathrm{Q}_{\mathrm{C}}=0$ as it is an adiabatic process
Therefore,
$\Rightarrow \Delta \mathrm{Q}_{\mathrm{C}}=\Delta \mathrm{U}_{\mathrm{C}}+\Delta \mathrm{W}_{\mathrm{C}}$
$\Rightarrow \Delta \mathrm{U}_{\mathrm{C}}=-\Delta \mathrm{W}_{\mathrm{C}}=\mathrm{n} \mathrm{C}_{\mathrm{v}} \Delta \mathrm{T}=\dfrac{\mathrm{P}_{\mathrm{o}} \mathrm{V}_{\mathrm{o}}}{\mathrm{RT}_{\mathrm{o}}} \times 2 \mathrm{R} \times\left(\dfrac{3 \mathrm{T}_{\mathrm{o}}}{2}-\mathrm{T}_{\mathrm{o}}\right)=\mathrm{P}_{\mathrm{o}} \mathrm{V}_{\mathrm{o}}$
$\Rightarrow \Delta \mathrm{U}=\Delta \mathrm{U}_{\mathrm{A}}+\Delta \mathrm{U}_{\mathrm{B}}+0 \quad$
Therefore, no heat change occurs in case of compartment C
$\Rightarrow \Delta \mathrm{W}=\Delta \mathrm{W}_{\mathrm{A}}+0+\Delta \mathrm{W}_{\mathrm{C}} \quad$
Hence, no change in volume in case of compartment B and therefore work done =0
The heat supplied by the heater = The heat supplied to compartment A + The heat flow through piston
$\Rightarrow \Delta \mathrm{Q}=\Delta \mathrm{U}_{\mathrm{A}}+\Delta \mathrm{U}_{\mathrm{B}}+\Delta \mathrm{W}_{\mathrm{AB}}=\Delta \mathrm{U}_{\mathrm{A}}+\Delta \mathrm{U}_{\mathrm{B}}+\Delta \mathrm{W}_{\mathrm{A}}=2 \Delta \mathrm{U}_{\mathrm{A}}+\Delta \mathrm{W}_{\mathrm{A}}$
$\Rightarrow \Delta \mathrm{Q}=18 \mathrm{P}_{\mathrm{o}} \mathrm{V}_{\mathrm{o}}$

Therefore, the correct answer is Option A.

Note: We must have a thorough knowledge on thermodynamics and we must read the given figure carefully. At first glance, the image might seem to be like a circuit but we must read the question thoroughly before deducing.