Question
Question: The figure shows an ideal pulley block of mass m (1 kg), resting on a rough ground with friction coe...
The figure shows an ideal pulley block of mass m (1 kg), resting on a rough ground with friction coefficient μ=1.5 . Another block of mass M (11 kg) is hanging as shown. When the system is released, it is found that the magnitude of acceleration of point P on string is a. Find the value of 4a in m/s2 . (Assume g=10m/s2 )
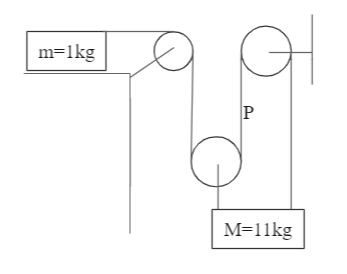
Solution
In a pulley system attached with masses, the total force acting on the body depends on the tension exerted on the strings of the pulley. When the system is released, different components of the pulley experience different acceleration depending on their position.
Complete step by step answer:
Let us assume four points on the pulley-mass system. We know that the acceleration at point P is a. Let us suppose this acceleration is in the upwards direction, then the acceleration of point R will also be a, but in the downward direction as they are attached with the same string. This implies the body M will be going down with acceleration a.
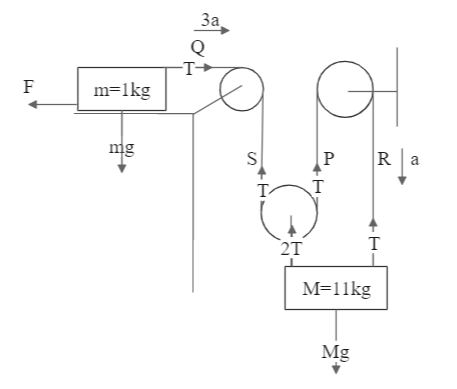
Now, the acceleration at point S will be given as:
2as+ap=−a [Negative because the direction of a is opposite to the accelerations at S and P]
⇒2as+a=−a
Hence, as=−3a
This implies that the direction of acceleration at S is in the downward direction. The block m will be under the same acceleration as they are connected with the same string joined by a fixed pulley.
Now, let us consider the block M with mass 11 kg. Doing the force balance on it, we get:
⇒Mg−T−2T=Ma
Putting in the values of M and g, we get:
⇒11×10−3T=11a [Eq. 1]
Moving on to the block m, we know that it experiences a frictional force which will be given as:
⇒F=μmg=1.5×1×10=15N
Performing the force balance on this block:
⇒T−F=m×3a
⇒T−15=3a
Substituting this value of T in the Eq. 1, we get:
⇒110−3(3a+15)=11a
⇒110−9a−45=11a
Solving for a:
⇒65=20a
Dividing both sides by 5
⇒13=4a
Hence, the value of 4a is 13m/s2 .
Note:
The pulley-system is used in mechanical systems to reduce the amount of force acting on heavy bodies so that they can be lifted easily. It works by redistributing the direction of the force acting on all the components of the system.
