Question

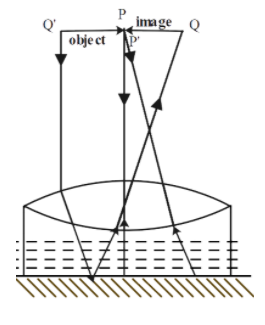
The figure shows an equiconvex lens (of refractive index 1.50) in contact with a liquid layer on top of a plane mirror. A small needle PO with its tip on the principal axis is moved along its axis until its inverted image is found at the position of the needle. The distance of the needle from the lens is measured to be 45.0cm. The liquid is removed and the experiment is repeated. The new distance is measured to be 30.0cm. The refractive index of the liquid is:

A. 5/4
B. 9/8
C. 4/3
D. 6/5

Answer 1

We have been asked to find the refractive index of the liquid. This can easily be done by using the lens maker’s formula. We will calculate focal length of a given lens and also of the lens and liquid system. We shall then calculate the radius of the given equiconvex lens and of the system. Using these values and the Lens maker’s formula we shall calculate the refractive index of the liquid in the system. The system will be the plano-concave lens formed by the lens liquid and plane mirror.

Formula Used:
$\dfrac{1}{f}=\left( \mu -1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)$ ,
Where,
f is the focal length
$\mu$= the refractive index
${{R}_{1}}$ and ${{R}_{2}}$ - radius of surface 1 and surface 2
$\dfrac{1}{f}=\dfrac{1}{{{f}_{1}}}+\dfrac{1}{{{f}_{2}}}$ ,
Formula for equivalent focal length.

Complete answer:
It is given that the image is formed at the same distance as the object. Therefore, we know, that equivalent focal length of system say $f$ = 45cm
Similarly, when the liquid is removed we are left with an equiconvex lens which also forms the image at the same distance as the object. Therefore, we can say that the focal length of the lens says ${{f}_{1}}$=30 cm.
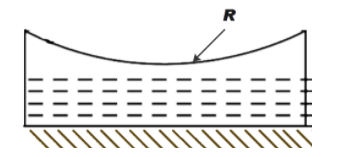
Therefore, now using the formula for equivalent focal length we can find the focal length of plano concave lens formed by the lower half of convex lens, the liquid and plane mirror (as shown in fig. below)

We know,
$\dfrac{1}{f}=\dfrac{1}{{{f}_{1}}}+\dfrac{1}{{{f}_{2}}}$
Now substituting given values,
We get,
$\dfrac{1}{45}=\dfrac{1}{30}+\dfrac{1}{{{f}_{2}}}$
$\Rightarrow \dfrac{1}{{{f}_{2}}}=\dfrac{2-3}{90}$
Therefore,
${{f}_{2}}$ = -90 cm
Now we can find the refractive index of liquid the Lens Maker’s formula
We know,
$\dfrac{1}{f}=\left( \mu -1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)$ …………………………. (1)
So for the system $f$= ${{f}_{2}}$ = -90 cm, $\mu$ = ${{\mu }_{2}}$, ${{R}_{1}}$= radius of the lower part of the equiconvex lens i.e. = -R
We know, radius of plane mirror ${{R}_{2}}$ = $\infty$
Now, substituting above values in (1)
We get,
$\dfrac{1}{{{f}_{2}}}=\left( {{\mu }_{2}}-1 \right)\left( \dfrac{1}{-R}+\dfrac{1}{\infty } \right)$
$\dfrac{1}{{{f}_{2}}}=\left( {{\mu }_{2}}-1 \right)\left( \dfrac{1}{-R}+0 \right)$ …………….. (2)
We have been given that the lens is equiconvex. Therefore, the radius of the upper half will be equal to the radius of the lower half.
Therefore, to find the radius of equiconvex lens
Using Lens Maker’s formula
$\dfrac{1}{{{f}_{1}}}=\left( {{\mu }_{1}}-1 \right)\left( \dfrac{1}{R}-\dfrac{1}{-R} \right)$
After substituting the values
We get,
$\dfrac{1}{30}=\left( 1.5-1 \right)\left( \dfrac{1}{R}+\dfrac{1}{R} \right)$
On solving above equation,
We get,
$\dfrac{1}{30}=\left( 1.5-1 \right)\dfrac{2}{R}$
Therefore,
$R=30cm$
Now, let us substitute the calculated value of R in equation (2)
${{\mu }_{2}}=\dfrac{30}{90}+1$
Therefore,
${{\mu }_{2}}=\dfrac{4}{3}$

Therefore, the correct answer is option C.

Note: Refractive index is the measure of bending of light ray when passing from one medium to another. Higher refractive index basically means that the light will travel slowly in the given medium, which leads to more bending in the light ray. The Equiconvex lens, as the name suggests, is the convex lens having equal distance from its centre axis to both surfaces.