Question
Question: The figure shows a uniform ramp between two buildings that allow for motion between the buildings du...
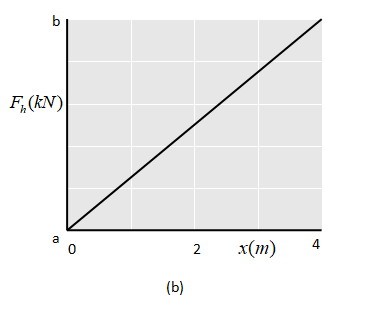
The figure shows a uniform ramp between two buildings that allow for motion between the buildings due to strong winds. At its left end, it is hinged to the building wall; at its right end, it has a roller that can roll along the building wall. There is no vertical force on the roller from the building, only a horizontal force with magnitude Fh . The horizontal distance between the buildings is D=4.00m . The rise of the ramp is h=0.490m . A man walks across the ramp from the left. The figure gives Fh as a function of the horizontal distance x of the man from the building at the left. The scale of the Fh axis is set by a=20kN and b=25kN . What are the masses of (a) the ramp and (b) the man?
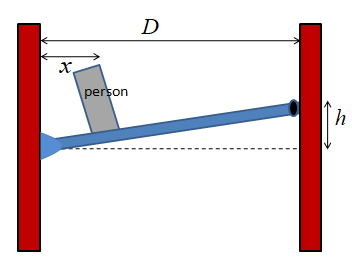

Solution
The whole system is considered to be in static equilibrium. Therefore the system must satisfy the condition for equilibrium. The first condition for equilibrium is the net force on the object must be zero. The second condition of the equilibrium is that net external torque is calculated. There are three external forces acting on the system. One is the weight of the man and the next is the weight of the ramp and the last one is horizontal. Therefore the sum of all these forces is zero.
Complete Step By Step Answer:
The horizontal distances between the buildings are given by, D=4.00m
The rise of the ramp is given by, h=0.490m
The most basic formula to calculate torque is to multiply Newton's force exerted by the meters of distance from the axis.
Therefore according to the second condition of equilibrium we get,
−mgx−Mg2D+Fhh=0 ……. (1)
Here, m is said to be the mass of the man
x is the distance between the man and the right building
M is said to be the mass of the ramp
h is the height by which the ramp is lifted
Fh is the leftward push. This equation can be written in the form of the equation of the straight line in a graph.
Fh= (slope ×x ) +y− intercept ……. (2)
Equation (1) can be rewritten as,
Fh=hmgx+Mg2hD ……. (3)
Since these two equations (2) and (3) have the same L.H.S we can compare the equations on the R.H.S.
Therefore we get,
The slope that can be represented as m ,
m=hmg ……. (4)
y-intercept that can be represented as, b=2hMgD …….. (5)
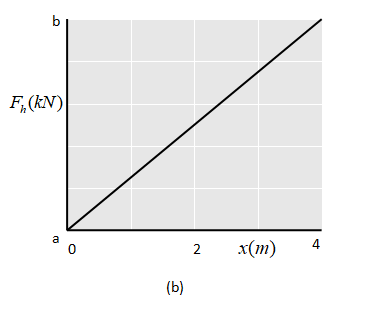
The y-intercept from the diagram is the point “ a ” which is given by a=20kN . Therefore we can substitute this value for “ b ” in the above equation.
Also, we have the values for D , h . We can substitute those to get the value for the mass of the ramp. That is, M .
Rearranging equation (5) we get,
gD2bh=M
⇒9.8×42(20,000)(0.490)=M
⇒M=500kg
Now rearranging the equation (4) we get,
gslope×h=m ….. (6)
From the graph, we can calculate the slope as,
Slope =4m5000N=1250N/m
Therefore substituting this in the equation (6) we get,
101250×0.490=m
⇒m=61.2kg
Correct Answer:
Therefore the mass of the ramp is given by, M=500kg and the mass of the man is given by, m=61.2kg .
Note:
We have introduced a negative sign while writing an equation for torque. This is due to the sign convention for torque. A common convention for the torque acting in the direction of counterclockwise we use positive sign and for the torque acting in the direction of clockwise, we use negative sign. The SI unit for torque is Newton times meters that can be written as N.m .
