Question
Question: The figure shows a thin metallic triangular sheet ABC. The mass of sheet is M. The moment of sheet a...
The figure shows a thin metallic triangular sheet ABC. The mass of sheet is M. The moment of sheet about side AC is:
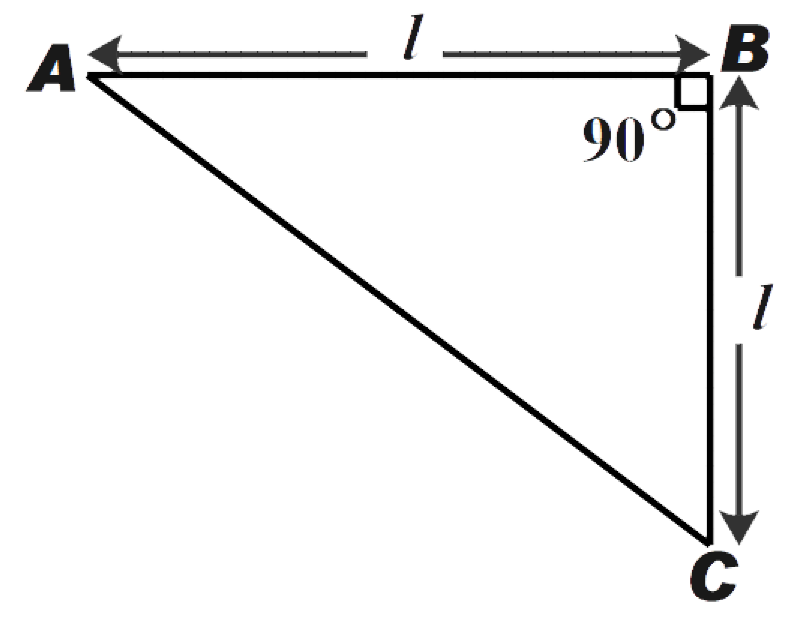
A. 18MI2
B. 12MI2
C. 6MI2
D. 4MI2
Solution
In this question we have been asked to calculate the moment of inertia about side AC in the given triangular sheet. To solve this question, we shall convert the triangle into square with sides of length l. Later, we shall calculate the MOI about the axis passing through the centre of mass and perpendicular to the sheet. We shall then use a perpendicular axis theorem to calculate the MOI about side AC.
Complete answer:
First let us convert the triangle into a square as shown in the figure below. So, if the triangle is unfolded as shown its mass can be said to be 2M as the given mass is M.
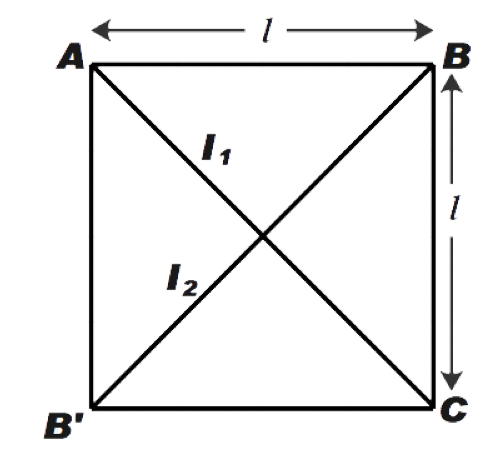
Now, we know that the moment of inertia of a square plate say I is given by
I=6(2M)×l2
Therefore,
I=3Ml2 …………….. (1)
Now, as shown in the figure above we know that I1 and I2 are perpendicular to each other.
Therefore,
From perpendicular axis theorem
We get,
I=I1+I2
Since I1 and I2 are symmetric, we can say that,
I1=I2
Therefore,
I=2I1
After substituting for I
We get,
I1=6Ml2
Now I1 is the moment of inertia of the square plate about the diagonal AC. Therefore, if the square is converted back into triangle we can say that the moment of inertia about the side AC say IACwill be half the calculated value of I1
Therefore,
IAC=21I1
After substituting the value
We get,
IAC=21×6Ml2
Therefore,
IAC=12Ml2
So, the correct answer is “Option B”.
Note:
Moment of inertia is the tendency of a body to resist any angular acceleration of the body. Moment of inertia also known as angular mass is given as the product of mass of the body and the square of its perpendicular distance from the axis about which the body is said to rotate. The perpendicular axis theorem states that moment of inertia of a planar body about an axis perpendicular to plane of body is equal to the sum of moment of inertia of two perpendicular axes, in the same plane as the body.
