Question

The figure shows a system of two concentric spheres of radii ${r_1}$ and ${r_2}$ and kept at temperature ${T_1}$ and ${T_2}$ respectively. The radial rate of flow of heat in a substance between the two concentric spheres, is proportional to:

A) $\dfrac{{\left( {{r_2} - {r_1}} \right)}}{{\left( {{r_1}{r_2}} \right)}}$
B) $\ln \left( {\dfrac{{{r_2}}}{{{r_1}}}} \right)$
C) $\dfrac{{\left( {{r_1}{r_2}} \right)}}{{\left( {{r_2} - {r_1}} \right)}}$
D) $\left( {{r_2} - {r_1}} \right)$

Answer 1

Consider a concentric spherical shell of some radius $r$ and width $dr$ between the two given shells and assume some that the shell is at some temperature $T$ . Calculate the heat flow through this shell and then integrate it from radius ${r_1}$ to radius ${r_2}$ . Accordingly, the radial rate of flow of heat in a substance between the two concentric spheres will be found.

Complete step by step solution:
In order to obtain the rate of heat flow between the given shells, let us calculate the rate of radial heat flow for a spherical surface between the two surfaces.

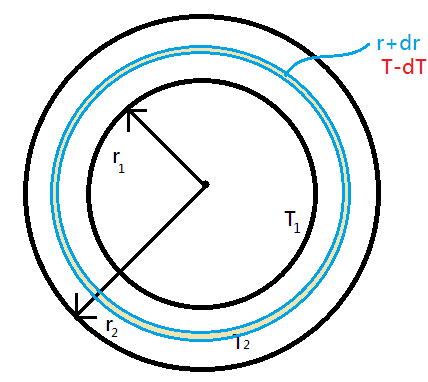
Here, we have considered a shell of radius $r$ and the width of the shell is $dr$ .
The shell is at temperature $T$ . Now, as the shell has some width, there will be some temperature difference between the inside and outside layer of the shell. This difference is because heat is flowing radially outwards. Naturally the temperature on the inner side of the layer will be more than the temperature on the outer side.

Let this temperature difference be $dT$. The rate of heat flow $\dfrac{{dQ}}{{dt}} = H$ through this spherical shell will be:
$H = \dfrac{{KAdT}}{{dr}}$
Here, $K$ is the conductivity of the material.
$A$ is the surface area of an object in contact. For the spherical surface the area will be $A = 4\pi {r^2}$
Substituting the value of area, we will get.
$H = \dfrac{{K\left( {4\pi {r^2}} \right)dT}}{{dr}}$
$H\dfrac{{dr}}{{{r^2}}} = 4\pi KdT$
Integrating on both sides, we get
$H\int\limits_{{r_1}}^{r2} {\dfrac{{dr}}{{{r^2}}}} = 4\pi K\int\limits_{{T_1}}^{{T_2}} {dT}$
The limits are taken as per the given values: when the radius is ${r_1}$ the temperature is ${T_1}$ and
When the radius is ${r_2}$ the temperature is ${T_2}$ .
Integrating and applying limits, we get
$H\left[ {\dfrac{1}{{{r_1}}} - \dfrac{1}{{{r_2}}}} \right] = 4\pi K\left[ {{T_2} - {T_1}} \right]$
as $\int\limits_{{r_1}}^{r2} {\dfrac{{dr}}{{{r^2}}}} = \left[ {\dfrac{1}{{{r_1}}} - \dfrac{1}{{{r_2}}}} \right]$ and $\int\limits_{{T_1}}^{{T_2}} {dT} = \left[ {{T_2} - {T_1}} \right]$
$\Rightarrow H\left[ {\dfrac{{{r_2} - {r_1}}}{{{r_1}{r_2}}}} \right] = 4\pi K\left[ {{T_2} - {T_1}} \right]$
$\Rightarrow H = \dfrac{{4\pi K\left[ {{T_2} - {T_1}} \right]}}{{\left[ {\dfrac{{{r_2} - {r_1}}}{{{r_1}{r_2}}}} \right]}}$
We need to find the relation between radial rate of heat flow and radius:
As $4\pi K\left[ {{T_2} - {T_1}} \right]$ is a constant therefore, we have
$H\alpha \dfrac{{{r_1}{r_2}}}{{\left( {{r_2} - {r_1}} \right)}}$
The radial rate of heat flow is proportional to $\dfrac{{{r_1}{r_2}}}{{\left( {{r_2} - {r_1}} \right)}}$ .

Therefore, option C is the correct option.

Note: We have assumed a spherical surface which is concentric with the given circles. The radial rate of heat flow is constant. The limits of the integral are taken as the given quantities of the smaller spherical shell and the given quantities of the bigger spherical shell.