Question
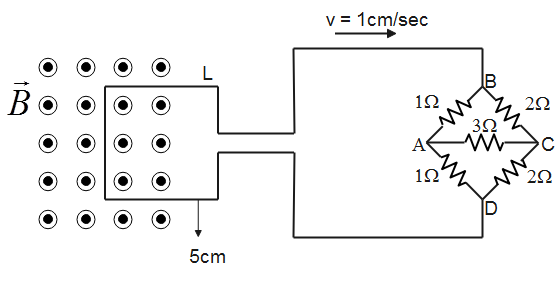
Question: The figure shows a square loop L of side \(5cm\) which is connected to a network of resistances. The...
The figure shows a square loop L of side 5cm which is connected to a network of resistances. The whole setup is moving towards right with a constant speed of 1cms−1. At some instant, a part of L is in a uniform magnetic field of 1T, perpendicular to the plane of the loop. If the resistance of L is 1.7Ω, what will be the approximate current in the loop at that instant?
A. 115μA
B. 170μA
C. 60μA
D. 150μA
Solution
First, calculate the total resistance of the loop. The network of resistors appears to be a Wheatstone bridge. Varying magnetic flux through the loop induced emf. Use the expression of motional emf to find the emf induced. The motional emf is equivalent to voltage across the circuit. Use Ohm’s law to obtain electric current in the loop.
Formula used:
Ohm’s law, V=IR
Complete step by step answer:
First, we shall calculate the resistance of the loop. We can note that the resistances between B and D are in Wheatstone bridge form as
RADRBA=RCDRBC
Therefore, the 3Ω resistance can be neglected as no current flows through it.
Now the circuit becomes as shown below.
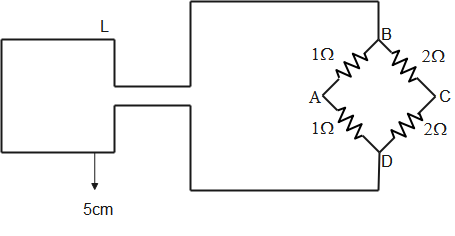
The resistances RBA and RAD; and RCA and RCD are in series and therefore can be replaced with single resistance equivalent to sum of their resistances. Now the circuit can be redrawn as shown below.
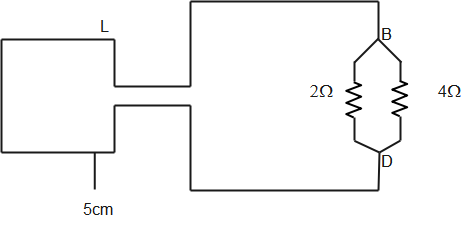
We can note that, the 2Ω and 4Ω are in parallel and their equivalent resistance is given by
Req1=21+41=43
⇒Req=34Ω≈1.3Ω
Given that the resistance of L is 1.7Ω. Therefore, net resistance through the loop is Rloop=1.7+1.3≈3Ω
Emf induced in a loop with its area vector along magnetic field and moving perpendicular to the magnetic field is given by
ϵ=Blv
Where b is the magnetic field and l is the length which is perpendicular to motion of the loop.
Substituting the values, we have
ϵ=1T×5cm×1cm/s=5×10−4Tm2/s
Current through the loop,
I=Rloopϵ=3Ω5×10−4V=1.67×10−4A≈170μA
Therefore, option B is correct.
Note:
Varying magnetic field induces electric current and therefore induces electric field. If magnetic flux through the loop is not changing, induced current will be zero.
Some basic conversions are often required in numerical problems. So, learn about milli-, centi-, micro-, kilo- etc.
