Question
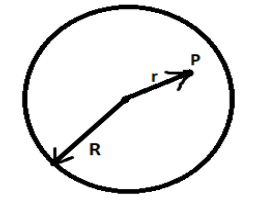
Question: The figure shows a sphere of radius r that carries a total charge Q uniformly distributed throughout...
The figure shows a sphere of radius r that carries a total charge Q uniformly distributed throughout its volume.
Which of the following expressions gives the electric field strength at point P, a point that lies inside the sphere and is a distance r from the center of the sphere?
A) E=4πε0R3Qr
B) E=4πε0r2Q
C) E=0 (Point P is inside of conductor)
D) E=4πε0R33Qr
Solution
We can consider a Gaussian surface for point P and distance from center become radius for this surface. We can use the following relationship to calculate electric strength at point P.
ϕ=E∬da where ϕ and E is electric flux and field respectively and ∬da is surface integral or area of the body.
ϕ=ε0q where q is the charge.
Volume charge density of a Gaussian surface is :
Volume of bodyCharge in body×Volume of Gaussian surface .
Formula used:
Area of sphere = 4πr2
Volume of sphere = 34πr2
Complete step by step answer:
Drawing a Gaussian surface around point P to get the electric flux:
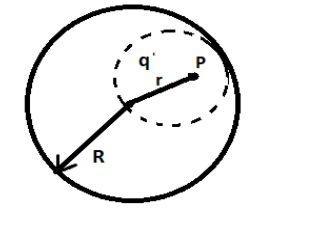
Let charge be enclosed in this Gaussian surface. Then according to Gaussian theorem, the flux inside this surface is given as:
ϕ=E∬da
For a square, the area will be 4πr2 so:
∬da=4πr2 [r being distance from center for P]
⇒ϕ=E×4πr2 ……… (1)
According to Gauss’ s law, the electric flux is equal to ε01 times the charge contained.
The charge contained in the Gaussian surface is, so:
ϕ=ε0q′ ………….. (2)
As both (1) and (2) represent electric fields for the Gaussian surface, they will be equal.
\Rightarrow E \times 4\pi {r^2} = \dfrac{{q'}}{{{\varepsilon _0}}} \\\
\implies E = \dfrac{{q'}}{{4\pi {r^2}{\varepsilon _0}}}......(3) \\\
Now, the charge enclosed by this Gaussian surface is the volume charge density of the sphere.
Volume of sphere is 34πr3 and the charge contained in the sphere is Q, so:
q' = \dfrac{Q}{{\dfrac{4}{3}\pi {R^3}}} \times \dfrac{4}{3}\pi {r^3} \\\
q' = Q\dfrac{{{r^3}}}{{{R^3}}} \\\ [r is radius of Gaussian surface and R is radius of the sphere]
Substituting this value in (3), we get:
E = \dfrac{1}{{4\pi {\varepsilon _0}{r^2}}} \times Q\dfrac{{{r^3}}}{{{R^3}}} \\\
E=4πε0R3Qr
Therefore, the electric field strength at point P, that lies inside the sphere at distance r from the center of the sphere is E=4πε0R3Qr and the correct option is A).
So, the correct answer is “Option A”.
Note:
The Gaussian surface is basically a 3-D space to calculate flux of electric fields.
Electric field in general terms is the rate of flow of electric field lines flowing in/out the given surface.
Flux can be produced on the spherical Gaussian surface due to a point charge, or shell with uniform charge distribution or symmetrical charge distribution.
