Question

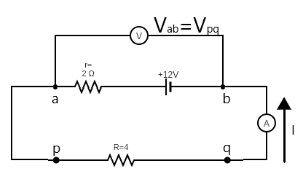
The figure shows a source (a battery) with an emf $E$ of 12 V with an internal resistance $r$ of $2\Omega$ and an external resistance of $4\Omega$ is added to complete the circuit. What are the voltmeter and the ammeter readings?

Answer 1

The internal resistance acts to reduce the emf of the battery detected by the voltmeter. So the voltmeter will show a reading less than the emf of the battery. Kirchhoff’s voltage rule can be used for the loop. So by that we will get the current in the circuit.

Formula used: In this solution we will be using the following formulae;
$\Rightarrow \sum V = 0$ where $V$ is the voltage across the individual element of the loop. $V = IR$ where $V$ is the voltage across a resistor, $I$ is the current flowing through the resistor, and $R$ is the resistance of the resistor.

Complete step by step solution:
Every cell or battery possesses an internal resistance which acts to reduce the actual emf the charges of the cell or battery produce. This internal resistance acts as though a resistor is connected in series to the ideal cell.
To calculate the voltage in the voltmeter and current in the ammeter, we must apply Kirchhoff’s rule to the loop to find the current. Hence we have
$\Rightarrow E - Ir - IR = 0$ where $E$ is the emf of the cell, $I$ is the current flowing through the circuit, $r$ is the internal resistance and $R$ is the resistance of the external resistor.
Inserting known values and calculating for $I$ we have,
$12 - 2I - 4I = 0$
On adding the like terms we get,
$\Rightarrow 6I = 12$
Hence, by dividing both sides by 6
$\Rightarrow I = 2{\text{A}}$
The voltmeter reading is simply the voltage across the 12 V emf and the internal resistance. Hence,
$\Rightarrow {V_{ab}} = E - Ir$
Hence, by inserting known values, we have
$\Rightarrow {V_{ab}} = 12 - 2\left( 2 \right) = 12 - 4$
$\therefore {V_{ab}} = 8{\text{V}}$
Therefore, the voltmeter reading and the ammeter reading are $8{\text{V}}$ and ${\text{2A}}$ respectively.

Note:
From the Kirchhoff’s voltage rule, we see that the voltage ${V_{ab}}$ must be equal to the voltage drop ${V_{pq}}$ across resistor $R = 4\Omega$ so that the voltage left after the complete loop is zero.
Mathematically, we have that
$\Rightarrow {V_{ab}} - {V_{pq}} = 0 \Rightarrow {V_{ab}} = {V_{pq}} = IR$
$\Rightarrow \therefore {V_{ab}} = IR$
Hence, alternatively, we calculate voltage ${V_{ab}}$ as
$\therefore {V_{ab}} = 4 \times 2 = 8V$ which is identical to the answer in solution.