Question

The figure shows a smooth circular path of radius R in a vertical plane which subtends an angle $\dfrac{\pi }{2}$ at O. A block of mass M is taken from position A to B under the action of a constant horizontal force F.

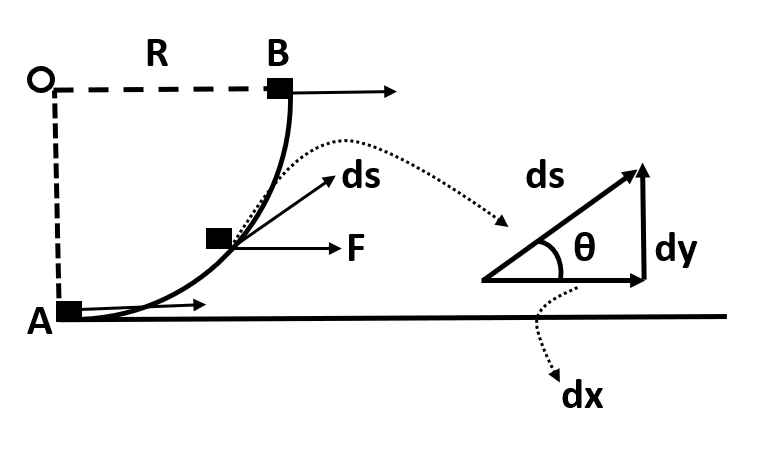
(a) Find the work done by this force
(b) In part (a), if the block is being pulled by a force F of constant magnitude which is always tangential to the surface, find the work done by the force F between A and B.

Answer 1

The work done by a force over a displacement is given as the scalar product of the force vector and the displacement vector. This means that if the force applied and displacement are along the same direction, then the net work done is simply their product. Also, if the force applied and displacement are perpendicular to each other, then by vector formula the net work done by that force is equal to zero.

Complete answer:
(a) In the first part of the question we have been asked to find out the work done by the constant force F in taking the block from A to B. To find this quantity, we can use the work formula stated as below:
$\begin{aligned} & \Rightarrow W=\int \overrightarrow{F}.\overrightarrow{dx} \\\ & \Rightarrow W=\overrightarrow{F}\int \overrightarrow{dx} \\\ \end{aligned}$
Here,
$\overrightarrow{F}$ is the applied force which is given to be constant.
$\overrightarrow{dx}$ is the displacement vector.
Since, work is the scalar product of these two vectors, the displacement along the direction of force will come into account in the equation and the displacement perpendicular to the direction of force will be equal to zero, that is:
$\Rightarrow \int \overrightarrow{dx}=R$
Therefore, the net work done is equal to:
$\Rightarrow W=FR$
Hence, the work done by the constant force F in taking the block from A to B is FR.
(b) In the second part we have, the force is always tangential to the surface. This means that at all times Force and displacement are parallel.
In this case, the displacement of the block along the direction of force is the length of the arc which is given by:
$\begin{aligned} & \Rightarrow \int \overrightarrow{dx}=\dfrac{2\pi R}{4} \\\ & \Rightarrow \int \overrightarrow{dx}=\dfrac{\pi R}{2} \\\ \end{aligned}$
So, the work done can be calculated using the same formula, that is:
$\Rightarrow W=\overrightarrow{F}\overrightarrow{\int dx}$
Putting the values of vector F and displacement, we get:
$\begin{aligned} & \Rightarrow W=F\left( \dfrac{\pi R}{2} \right) \\\ & \Rightarrow W=\dfrac{\pi FR}{2} \\\ \end{aligned}$
Hence, the work by the Force in taking the block from A to B when acting along the surface is equal to $\dfrac{\pi FR}{2}$.

Note:
One should easily tell the direction of displacement of any particle in the question as doing so will solve the hardest part of our question. For example, if the particle would have been hanging from O, then the net work done by tension would have been zero. As, tension and displacement at any instant would be perpendicular. This is how we need to visualize problems quickly and correctly.