Question

The figure shows a series LCR circuit with $L = 54H$ , $C = 80\mu F$ , $R = 40\Omega$ connected to a variable frequency $240V$ source, calculate:
(A) The angular frequency of the source which drives the circuit at resonance,
(B) The current at the resonating frequency,
(C) The rms potential drops across the inductor at resonance.

Answer 1

Draw the circuit diagram for the given condition. The angular frequency is inversely proportional to the product of square root of Inductance and capacitance. At resonating frequency, we have $\omega L = \dfrac{1}{{\omega C}}$ hence now impedance can be calculated and hence the current can also be calculated.

Complete step by step solution:
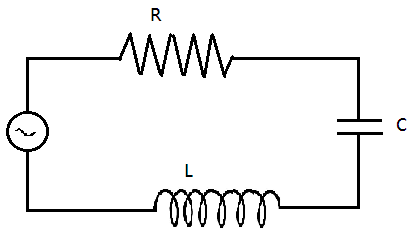
Let’s draw the circuit first with the values of resistance, conductance and inductance.

The above image shows a LCR series circuit.
(A) The angular frequency is also known as resonance frequency and is depicted as ${\omega _r}$ , the angular frequency is given as:
${\omega _r} = \dfrac{1}{{\sqrt {LC} }}$
Substituting the values of inductance and capacitance from the given question, we have:
$\Rightarrow {\omega _r} = \dfrac{1}{{\sqrt {54 * 80 * {{10}^{ - 6}}} }}$
$\Rightarrow {\omega _r} = 15.2rad/s$
Hence the angular frequency is ${\omega _r} = 15.2rad/s$

(B) To calculate the current in LCR circuit at resonance we must understand that at resonant frequency the magnitude of inductance and capacitance is equal and hence the only impedance is due to the resistance. Taking this into account we can calculate the impedance as follows:
$Z = R$
Where $Z$ is impedance and $R$ is the resistance.
Now current is given as:
$I = \dfrac{V}{Z}$
Where $I$ is the current.
$\Rightarrow I = \dfrac{V}{R}$ since $Z = R$
Substituting the values, we have
$\Rightarrow I = \dfrac{{240}}{{40}}$
$I = 6A$
Therefore, the value of current at resonating frequency is $I = 6A$

(C) The peak voltage will be given as:
${V_0} = \sqrt 2 V$
Where ${V_0}$ indicates the peak voltage.
Similarly the peak current will be ${I_0} = \dfrac{{\sqrt 2 V}}{Z}$ where ${I_0}$ is the peak current
$\Rightarrow {I_0} = \dfrac{{\sqrt 2 (240)}}{{40}}$
$\Rightarrow {I_0} = 8.49A$
Hence at resonance the impedance of the circuit is $40\Omega$ and the amplitude of the current is ${I_0} = 8.49A$.
The rms potential drop across the inductor:
${V_{L(rms)}} = I {\omega _r}L$
Where ${V_{L(rms)}}$ is the potential drop at rms across inductance;
${\omega _r}$ is the angular frequency or resonance frequency
Therefore, potential drop is
${V_{L(rms)}} = 6 * 15.2 * 54$
$\Rightarrow 4934.2V$

Note: It is to be noted that the potential drop across the capacitance is also $4934.2V$ hence the potentials of capacitance and inductance are equal. The potential drop across the capacitance can be calculated as $I(\dfrac{1}{{\omega C}})$. Be careful while substituting the values and avoid making calculation errors. While solving the question do remember that the value of capacitance is in microfarads.