Question
Question: The figure shows a potentiometer in which \[R\] is a variable resistance and \[\text{AB}\] is a unif...
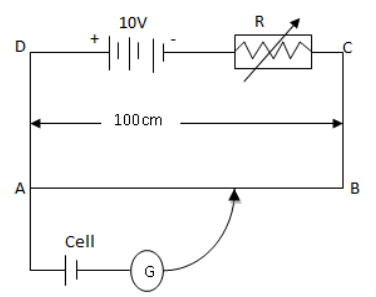
The figure shows a potentiometer in which R is a variable resistance and AB is a uniform wire of length 100cm having resistance r. In an experiment when R=0 the null point is obtained at 30cm from end A.For another value of R, the null point is obtained at 60cm from A. Find the value R in the second case.
Solution
Galvanometer is a device that is used to measure presence of electric current. Null deflection in the galvanometer indicates that there is no current flowing through the galvanometer. Using this concept we can find the value of R in the second case.
Formula used:
According to Ohm’s law we have,
V=IR
Where V is the voltage, I is the current and R is the resistance.
Complete step by step answer:
Given a uniform wire AB of length, L=100cm.
Resistance of the whole wire is r.
The EMF of the battery is E=10V.
Also, in the figure a galvanometer is used with a movable jockey along the wire AB.
In the first case, the value of R is R=0 and the null point is at l1=30cm.
In the second case, the null point is at l2=60cm.
Let the total current through the circuit be I.In first case, the null point is at l1=30cm which is the length between the point A and jockey which means there is no flow of current through the part length between point A and jockey and the current flows through the part of wire between the jockey and point B. The length between jockey and point B is
l1′=l−l1
Putting the values of l and l1 we get,
l1′=100−30=70cm
The wire is uniform and for 100cm the resistance is r.
For 1cm the resistance will be 100r
For 70cm the resistance will be r′=100r×70=107r
Now, the total resistance in the circuit is,
R1=R+r′
Putting the values of R and r′ we get
R1=0+107r
⇒R1=107r
Using Ohm’s law we get,
E=IR1
⇒I=R1E
Putting the values of E and R1 we get,
I=(107r)10
Now, the denominator’s denominator is multiplied in numerator
⇒I=7r10×10
⇒I=7r100 (i)
Similarly, in the second case the null point is at l2=60cm which is the length between the point A and jockey. So, the part of the wire through which the current flows is between the jockey and point B. The length between jockey and point B is
l2′=l−l2
Putting the values of l and l2 we get,
l2′=100−60=40cm
For 1cm the resistance will be 100r
For 40cm the resistance will be r′′=100r×40=104r
Now, the total resistance in the circuit is,
R2=R+r′′
Putting the values of r′′ we get
R2=R+104r
Using Ohm’s law we get,
E=IR2
⇒I=R2E
Putting the values of E and R2 we get,
I=(R+104r)10
Now, the denominator’s denominator is multiplied in numerator
⇒I=10R+4r10×10
⇒I=10R+4r100 (ii)
Equating equations (i) and (ii) we get,
7r100=10R+4r100
⇒7r1=10R+4r1
Cross multiplying the denominators,
⇒10R+4r=7r
⇒10R=7r−4r
Further Simplifying we get,
⇒10R=3r
∴R=103r
Therefore, the value R in the second case is 103r.
Note: Remember for a given material, the resistance of the material is directly proportional to its length, if the length increases, the resistance of the material increases and if the length decreases the resistance of the material decreases. Also, resistance is inversely proportional to the cross sectional area. In the above question the wire is uniform so the cross sectional area is constant.
