Question
Question: The figure shows a network of seven capacitors. If the charge on the 5μF capacitor is 10μC, the pote...
The figure shows a network of seven capacitors. If the charge on the 5μF capacitor is 10μC, the potential difference between the points A and C is given as 3x.
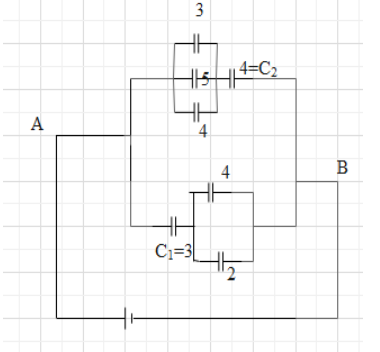
Solution
We should have knowledge about kirchhoff's law of capacitance for solving this circuit. Q=CV, we will deal with equivalent capacitance across two points. Charge conservation method should be kept in mind. We will find Qeq, Ceq and VAB and by using formula we will solve the question.
Formula used:
Qeq=CeqVAB
Complete answer:
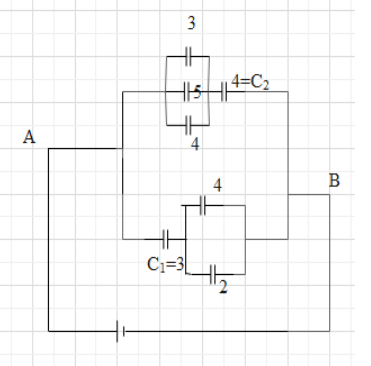
Firstly we will find potential across 5 capacitor
Let the potential across the 5μf capacitor be v5.
Potential across 5μf is v5=c5q5
=510=2
As we can see that(3μf,4μf,5μf) are in parallel in below given diagram
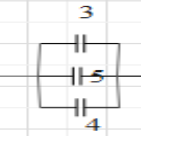
So now we will find charge on 3μf and 4μf capacitor voltage across both the capacitance will be the same as both are in parallel i.e =2volts.
Charge on 3μf is Q3=3×2=6μC
Charge on 4μf is Q44×2=8μC
Charge on 5μf is Q5=5×2=10μC
Now we can see that C2 is in series with (3μf,4μf,5μf)so charge on C2 and group (3μf,4μf,5μf)are same.
So we can find the charge on C2 is Q2=10+6+8=24μC
And potential across it V2=424=6V
Thus we will now find potential across point A and B
VAB=V5+V2=2+6=8V
Now equivalent capacitance of lower branch of circuit is
Ceq=3+4+23(4+2)=2μf And;
Total equivalent chargeQeq=CeqVAB=2(8)=16μC
∴VAC=3Qeq=316
Thus on comparing it with 3x we obtain x=16.
On solving the circuit by basic charge conservation method we obtain that x=16.
Note:
We have to apply charge conservation carefully properties of capacitor in series and parallel should be kept in mind
Formula to find the charge on capacitor is
q=CV
Where,
q=charge on capacitor
V= voltage applied across capacitor
C= Capacitance of capacitor
When voltage is applied across a parallel plate capacitor it produces positive charge on one plate and negative charge on another plate. Charge across the capacitor is directly proportional to voltage.
