Question
Question: The figure shows a network of capacitors where the numbers indicate capacitances in micro Farad. The...
The figure shows a network of capacitors where the numbers indicate capacitances in micro Farad. The value of capacitance C such that the equivalent capacitance between point A and B is to be 1μF is:
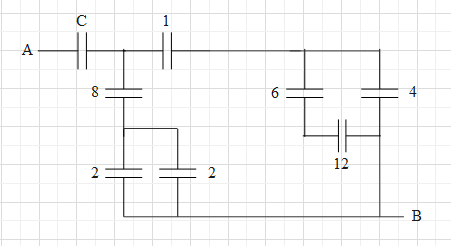
Solution
To solve the given question we must know when the capacitors are series and when they are parallel. Then we must also know the concept of effective capacitance of ‘n’ capacitors connected in series and effective capacitance of ‘n’ capacitors connected in parallel.
Formula used:
Ceq=C1+C2+C3+......+Cn
Ceq1=C11+C21+C31+....+Cn1
Complete step by step answer:
Let us first check which of the capacitors are in parallel and find their effective capacitance first. When two more capacitors are across the potential difference or they have the same positive and negative terminals, the capacitors are said to be in parallel connection.
When the n capacitors of capacitances C1,C2,C3,......Cn are in parallel connection, the effective capacitance of the combination is given as Ceq=C1+C2+C3+......+Cn.
In the given figure, we can see that the two capacitors of capacitance 2μF in parallel connection.
Therefore, the effective capacitance of the two is Ceq=2μ+2μ=4μF.
When the n capacitors of capacitances C1,C2,C3,......Cn are in series connection, the effective capacitance of the combination is given as Ceq1=C11+C21+C31+....+Cn1.
In the given figure, we can see that the capacitors of capacitance 6μF and 12μF in series connection.
Then we can write that Ceq1=6μ1+12μ1=4μ1
Therefore, the effective capacitance of the two is Ceq=4μF.
With this the circuit can be simplified as shown below.
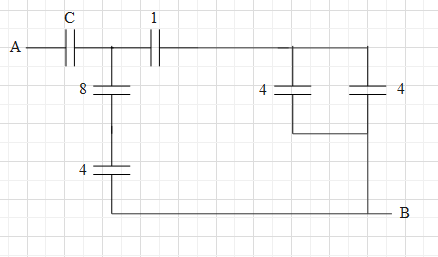
Now, we can see that the two 4μF capacitors are in parallel. Therefore, the effective capacitance of these two is Ceq=4μ+4μ=8μF.
And the capacitors of capacitances 8μF and 4μF in series connection. Therefore, the effective capacitance of these two is Ceq1=8μ1+4μ1=8μ3.
⇒Ceq=38μF
The circuit can be simplified further as shown.
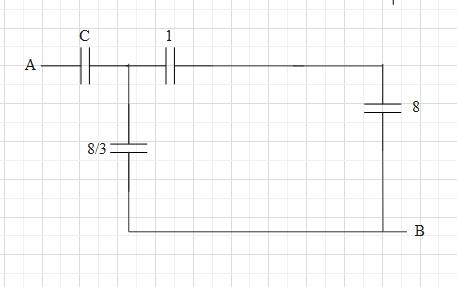
Now, the capacitors of capacitances 1μF and 8μF in series connection. Therefore, the effective capacitance of these two is Ceq1=1μ1+8μ1=8μ9.
⇒Ceq=98μF.
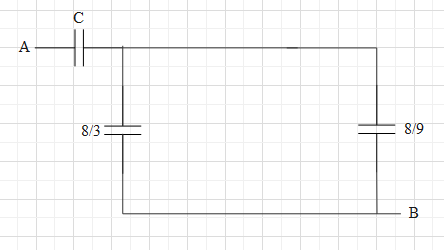
Now, the capacitors of capacitances 38μF and 98μF in parallel connection. Therefore, the effective capacitance of these two is Ceq=38μ+98μ=932μF.
Therefore, the circuit simplifies to:
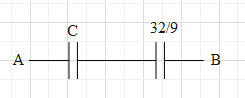
Therefore, the effective capacitance of the whole circuit is Ceq1=C1+32μ9.
But it is given that the effective capacitance of the whole circuit is 1μF.
⇒Ceq1=C1+32μ9=1μ1
⇒C1=1μ1−32μ9=32μ23
⇒C=2332μF
Therefore, the required value of capacitance C is 2332μF
Note:
The formulae for the effective capacitance of n capacitors and effective resistance of n resistors can be misunderstood.
The formula for effective resistance of n resistances in series is similar to the formula for effective capacitance of n capacitors in parallel.
The formula for effective resistance of n resistances in parallel is similar to the formula for effective capacitance of n capacitors in series.
