Question
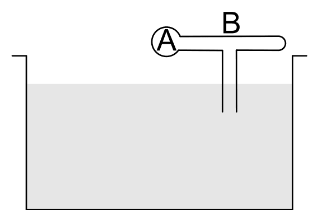
Question: The figure shows a model of perfume atomizer. When the bulb A is compressed, air flows through the n...
The figure shows a model of perfume atomizer. When the bulb A is compressed, air flows through the narrow tube consequently pressure at the position of the vertical tube reduces. The liquid (perfume) rises in through the vertical tube and emerges through the end. If the excess pressure applied to the bulb in this process be ΔP then the minimum speed of air in the tube to lift the perfume is
A. ρa2 (ΔP + ρgh)
B. ρa2 (ΔP − ρgh)
C. ρaΔP + ρgh
D. None of these
Solution
We will use the concept of gauge pressure. Then, we will perform some minute manipulations. Then we will finally find the equation of the required parameter. Finally, we will compare the evaluated equation with the given options and also manipulate if necessary.
Formula Used:
Po = P + ρgh
Where, Po is the atmospheric pressure, P is the pressure on a substance and ρgh is called the gauge pressure on the substance.
Energy per unit volume: 21 ρV2
Where, V is the volume of the substance.
Complete step by step answer:
The pressure on the bulb B can be written as the pressure on B summed up with the energy per unit volume due to A. Thus,
P = PB + 21 ρaV2 −−−−−−−−−− (i)
Again, the pressure on bulb B is the excess pressure summed up with the atmospheric pressure.Thus,
P = ΔP + Po −−−−−−−−−− (ii)
Using (ii) in (i), we get
ΔP + Po = PB + 21 ρaV2 −−−−−−− (iii)
Now, we can write,
PB + ρgh = Po
Further, we get
PB = Po − ρgh −−−−−−−−− (iv)
Using (iv) in (iii), we get
ΔP + Po = Po − ρgh + 21 ρaV2
Clearly, Po will cancel out from both sides. Thus, we get
ΔP = − ρgh + 21 ρaV2
Further, we get
ΔP + ρgh = 21 ρaV2
Then, we can write
2 (ΔP + ρgh) = ρaV2
Further, we get
ρa2 (ΔP + ρgh) = V2
Finally, we get
∴V = ρa2 (ΔP + ρgh)
Hence, the correct answer is B.
Additional information: Gauge pressure is the pressure which is excessive of the atmospheric pressure acting on a substance. Absolute pressure on a substance is simply the summation of the gauge pressure and the atmospheric pressure. This gauge pressure could be of any type. Let us say if an object is immersed in a liquid, then the gauge pressure here will be the pressure the liquid exerts on the walls of the object. Like this, the gauge pressure on an object will be dependent on the situation in which the object is kept in.
Note: Students should be very much cautious while substituting the value of gauge pressure as the gauge pressure is different in different cases. Students commit errors while manipulating the equations.
