Question

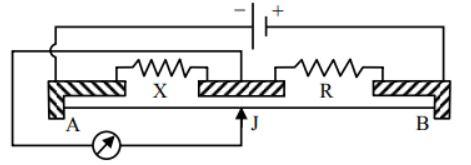
The figure shows a metre- bridge circuit, with $AB = 100\,cm$, $X = 12\,\Omega$ and $R = 18\,\Omega$ , and the jockey $J$ in the position of balance. If $R$ is now made $8\,\Omega$ , through what distance will $J$ have to be moved to obtain in balance?

(A) $10\,cm$
(B) $20\,cm$
(C) $30\,cm$
(D) $40\,cm$

Answer 1

Metre bridge is mainly used for the finding of the unknown resistance connected in the circuit. It uses the formula of the ratio of the known and the unknown resistance is equal to the ratio of the balancing length of the metre bridge. The difference of both lengths provides the value of the distance to be moved by a jockey.

Formula used:
In the meter bridge,
$\dfrac{X}{R} = \dfrac{l}{{100 - l}}$
Where $X\,and\,R$ are the value of the resistance in the meter bridge circuit, $l$ is the length of the circuit.

Complete step by step answer:
Given: Value of the resistance, $X = 12\,\Omega$
Value of the other resistance, $R = 18\,\Omega$
The length of the meter bridge circuit, $AB = 100\,cm$
Final value of the resistance, $R' = 8\,\Omega$
Using the formula of the metre bridge for the initial condition as
$\dfrac{X}{R} = \dfrac{l}{{100 - l}}$
Substituting the value of the known parameters in the above formula,
$\dfrac{{12}}{{18}} = \dfrac{l}{{100 - l}}$
By cross multiplying the terms in both left hand side and the right hand side of the equation,
$6\left( {100 - l} \right) = 18l$
$600 = 12l$
By further simplification,
$l = 50\,cm$
By substituting the final condition in the formula,
$\dfrac{{12}}{8} = \dfrac{{l'}}{{100 - l'}}$
By further simplification of the above equation, we get
$l' = 30\,cm$
The distance that the jockey is moved is calculated by the difference of the length of the circuit.
$l - l' = 50 - 30 = 20\,cm$

Hence, the correct answer is option (B).

Note: Metre Bridge works on the principle of the Wheatstone bridge and it is used for the purpose of the unknown resistance that is connected in the circuit by adjusting the jockey in between the resistors by using the balancing length.