Question
Question: The figure shows a horizontal force \(\vec F\) acting on the block of mass \(M\) on an inclined plan...
The figure shows a horizontal force F acting on the block of mass M on an inclined plane (angle θ ). What is the normal reaction N on the block?
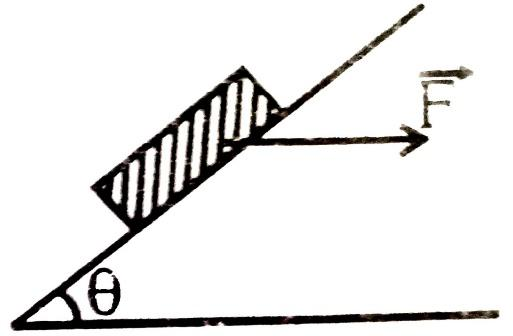
A) mgsinθ+Fcosθ
B) mgsinθ−Fcosθ
C) mgcosθ−Fsinθ
D) mgcosθ+Fsinθ
Solution
Construct the diagram of the horizontal force given and also the force due to the weight of the block taken. Split these two forces into horizontal components and the vertical component to obtain the resultant force and the normal force to it.
Complete step by step solution:
It is given that the
Horizontal force acting on the block is F
The mass of the block is M
The mass is at an angle of θ on the inclined plane
Since F is the horizontal force that acts on the block, it pushes the block to move upward on the slanting inclined plane. There will be the force which acts against it and downwards. It is formed by the combination of the weight of the block and the gravitational force of the block towards the earth. According to Newton's second law of motion, force is the product of the mass and the acceleration.
Fw=mg
This force pulls the block towards down against the horizontal external force. Let us construct the diagram of the case given.
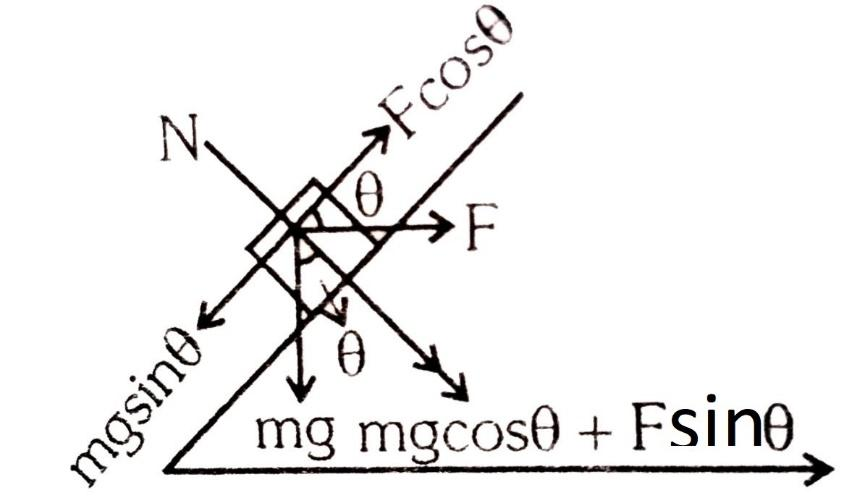
From the constructed diagram, the force mgdivided into mgsinθ and mgcosθ. And the horizontal force divided into Fsinθ and Fcosθ . If we take the normal, the answer is mgcosθ+Fsinθ.
Thus the option (D) is correct.
Note: It is to be noted that when the vector of the force is divided into the horizontal and the vertical component, the sine of the force magnitude is taken as the vertical component of force and the cosine is taken as the horizontal component.
