Question
Question: The figure shows a circular loop with radius \(r\). The resistance of arc ABC is \(5\Omega \) and th...
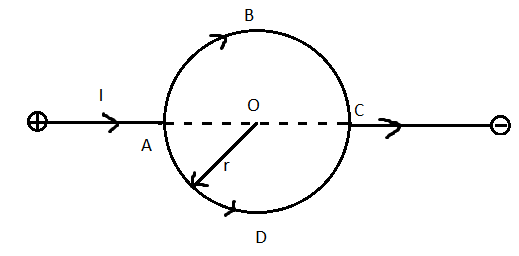
The figure shows a circular loop with radius r. The resistance of arc ABC is 5Ω and that of ADC is 10Ω. Magnetic field at the center of the loop is:
A.)3rμ0I⊗
B.)15rμ0I⊗
C.)12rμ0I⊙
D.)6rμ0I⊙
Solution
Hint: This problem can be solved by using the expression for the magnetic field due to a semicircular current carrying coil at its center, separately for arcs ABC and ADC. Both of them will have different currents based on their resistances. The sum of these two magnetic fields keeping in mind their directions using the right hand thumb rule, will give the total magnetic field at the center.
Formula used:
The magnetic field due to a current carrying semicircular coil at its center is given by
B=4Rμ0I
Where I is the current in the coil, R is the radius of the coil and μ0 is the permeability of free space.
The direction of the magnetic field is given by the right hand thumb rule which states that if we curl the fingers of our right hand in the direction of the current along the coil, our thumb points towards the direction of the magnetic field at the center.
When a current I splits into two branches, one with a resistance R1 and another with resistance R2, the respective currents I1 and I2 flowing through the two branches is given by,
I1=R1+R2R2I and I2=R1+R2R1I
Complete step by step answer:
Here we are given a circular coil and a current I branches into the two halves of the coil. Essentially, the circle can be considered as two parallel semi circular branches.
We will find out the magnetic field at the center of the coil due to the respective currents flowing in each branch and sum them up in the end to get the total magnetic field at the center.
The magnetic field due to a current carrying semicircular coil at its center is given by
B=4Rμ0I --(1)
Where I is the current in the coil, R is the radius of the coil and μ0 is the permeability of free space.
The direction of the magnetic field is given by the right hand thumb rule which states that if we curl the fingers of our right hand in the direction of the current along the coil, our thumb points towards the direction of the magnetic field at the center.
We will find out the currents flowing in each branch as a fraction of the total current by taking the resistance of each branch in consideration.
When a current Isplits into two branches, one with a resistance R1 and another with resistanceR2, the respective currents I1 and I2 flowing through the two branches is given by,
I1=R1+R2R2I and I2=R1+R2R1I --(2)
Hence, now let us analyze the question.
Let the resistance of the arc ABC be RABC.
We are given that RABC=5Ω.
Let the resistance of the arc ADC be RADC.
We are given that RADC=10Ω.
The total current entering the circular coil is given as I.
The radius of the coil is r.
Let the currents flowing in branches ABC and ADC be IABC and IADC respectively.
Therefore, using equation (2), we get,
IABC=RABC+RADCRADCI
∴IABC=5+1010I=1510I=32I ---(3)
Similarly, using (2), we get,
IADC=RABC+RADCRABCI
∴IABC=5+105I=155I=31I --(4)
Let the magnetic field at the center of the coil due to the current flowing in arc ABC and arc ADC be BABC and BADCrespectively.
Plugging in the values and using equation (1), and using (3) and (4) we get,
BABC=4rμ0IABC=314rμ0Iinto the plane of the screen (using the right hand thumb rule)
∴BABC=314rμ0I⊗ --(5)
where the symbol ⊗ means that the magnetic field points into the plane of the screen.
Similarly,
BADC=4rμ0IADC=324rμ0Iout of the plane of the screen (using the right hand thumb rule)
BADC=324rμ0I⊙ --(6)
where the symbol ⊙ means that the magnetic field points out of the plane of the screen.
The total magnetic field at the center is the sum of that due to the two branches. Hence,
B=BABC+BADC
where B is the required magnetic field at the center of the coil.
Therefore using the values form (5) and (6), we get,
B=314rμ0I⊗+324rμ0I⊙
=−314rμ0I⊙+324rμ0I⊙=314rμ0I⊙=12rμ0I⊙ [For a vector V (V⊗=−V⊙) ]
Hence, the required magnetic field value at the center is 12rμ0I⊙.
Hence, the correct option is C) 12rμ0I⊙.
Note: Students often forget to take into account that the magnetic fields produced by the currents in the two branches are opposite in direction and cancel each other out to an extent. They simply add up the two magnitudes without taking into account the direction. This leads to a completely wrong answer. An easy way to remember the meaning of the symbols ⊗ and ⊙ is to relate them to an arrow. The ⊗looks like the back of an arrow going away from you into the screen, and hence, the symbol ⊗ means that the direction of the vector is away from you into the plane of the screen.
Similarly, the ⊙ like the front pointed end of an arrow coming towards you out of the screen, and hence, the symbol ⊙means that the direction of the vector is towards you out of the plane of the screen.
