Question
Question: The figure shows a capillary tube of radius r dipped into water. The atmospheric pressure is\[{{P}_{...
The figure shows a capillary tube of radius r dipped into water. The atmospheric pressure isPo and the capillary rise of water is h. S is the surface tension for water-glass. Initially, h=10cm. If the capillary tube is now inclined at 45∘, the length of water rising in the tube will be
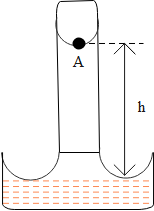
Explanation
Solution
We will make use of the height formula, that is, the capillary rise of liquid to compute the value of the rise in the liquid. The rise of the liquid formula is the initial height of the liquid present in the cube by the cosine of the angle by which the tube is tilted.
Formulae used:
